Recta Tangente.

Si se tiene una función $y = f (x)$ y la referencia de uno de sus puntos $P_T$ de coordenadas $(x_T ,\; y_T )$, donde $y_T=f(x_T),$
se define la recta tangente $l_T$ a la gráfica de la función $f(x)$ en el punto $P_T,$
como el límite de las rectas secantes que pasan por ese punto $P_T$ y otro punto $Q$ en la gráfica, que se hace tender hacia $P_T$.

Gráficamente:

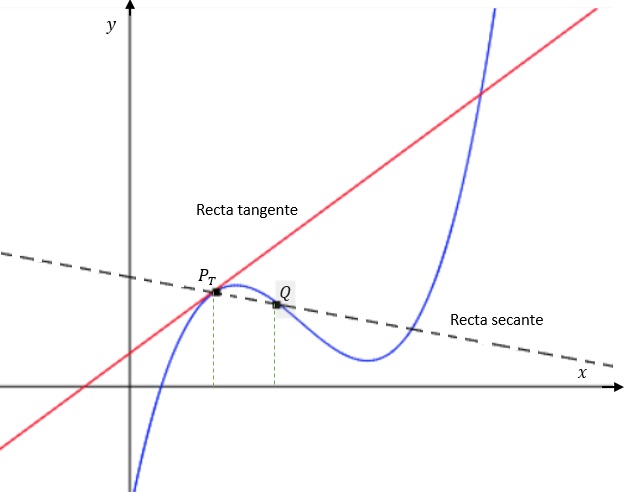
La recta secante pasa por los puntos $P_T=( x_T ,\;f(x_T ) )$ y el otro punto $Q$ de coordenadas $(x_T+h ,\;f(x_T+h) )$ donde $h$ es una cantidad que al hacerla tender a cero provocará que el punto $Q$ tienda hacia el punto $P_T$.

La pendiente de una recta, de la que se conocen dos puntos es $m=\frac{y_2-y_1}{x_2-x_1 }.$

Así la pendiente de la recta secante es $m_S=\frac{f(x_T+h)-f(x_T)}{x_T+h - x_T}=\frac{f(x_T+h)-f(x_T)}{h}$,

y la pendiente de la recta tangente será $m_T=\underset{h\to 0}{\lim}\frac{f(x_T+h)-f(x_T)}{h}$, ya que como se dijo, la tangente es el límite de las secantes.

Este límite se define como la derivada de la función $f(x)$ en el punto $x=x_T$ y se denota como:

$$f´(x_T)=\underset{h\to 0}{\lim}⁡\frac {f(x_T+h)-f(x_T)}{h}.$$

Ejemplo 1.

Dar un esbozo gráfico de la función $f(x)=4x-x^2$ y su recta tangente en $x = 1$ determinando gráficamente la recta tangente como el límite de las rectas secantes.

La función es un polinomio de segundo grado cuya gráfica es una parábola que abre hacia abajo (porque el coeficiente del término cuadrático es negativo) y que tiene raíces en $x = 0$ y en $x = 4$ (porque $f(x)=4x-x^2=x(4-x)=0$ para $x = 0$ y para $x = 4$) y vértice en $V (2 , 4)$ (porque la $x_V=\frac{-b}{2 a}=\frac{-4}{-2}=2$ y la $y_V=f(x_V )=f(2)=8-4=4$ ).

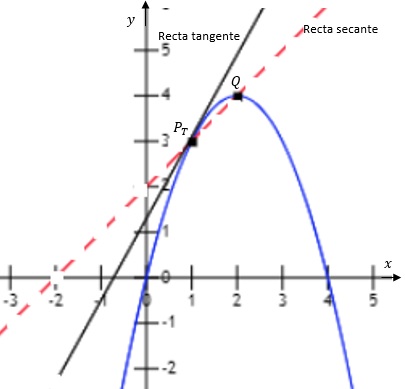
Las coordenadas del punto de tangencia son: $x_T=1\;\;$ y $\;\;y_T=f(1)=4(1)-(1)^2=3$, se tiene $P_T (1 ,3)$.

Ejemplo 2.

Obtener mediante la definición de la derivada, la ecuación de la recta tangente a $f(x)=4x-x^2$ en $x = 1$.

El punto de tangencia es $P_T (1 ,f(1)) = P_T (1 ,3)$ y la pendiente es $m_T=f´(1)$, en este caso:
$m_T= f´(1)= \underset{h\to 0}{\lim} \frac{f(1+h)-f(1)}{h}=\underset{h\to 0}{\lim} \frac{4(1+h)-(1+h)^2-3}{h} ∶\frac {0}{0} ∶ indeterminado $

$m_T⁡=⁡ \underset{h\to 0}{\lim} \frac{4+4h-(1+2h+h^2)-3}{h}=\underset{h\to 0}{\lim} \frac{4h-2h-h^2}{h}=\underset{h\to 0}{\lim} \frac{h(2-h)}{h}=\underset{h\to 0}{\lim} (2-h)=2 $

(La ecuación de una recta cuando se conoce su pendiente $y$ un punto es: $ y-y_1=m (x-x_1)$.

En este caso se tiene $m_T=2$ y $P_T (1 ,3)$ por lo que la ecuación de $l_T$ es:

$y-3=2(x-1)$
$y=2x-2+3$
$y=2x+1.$

Que coincide con lo que se ve en la gráfica del ejemplo 1, la recta tangente corta al eje $y$ en 1 y tiene pendiente 2.

(la pendiente se puede ver en la gráfica tomando en cuenta que $m=\frac{y_2-y_1}{x_2-x_1}=\frac{∆y}{∆x}$ y si fijamos $∆x=1\;\;\; m=∆y$, así en cualquier punto de la recta se toma 1 a la derecha y se ve cuanto se tiene que subir o bajar para alcanzar nuevamente a la recta, ese será el valor de la pendiente, si se sube es positiva y si se baja es negativa.

Ejemplo 3.

Obtener mediante la definición de la derivada, la ecuación de la recta tangente a $ f(x)=\frac{2x}{3x+5}$ en $x = – 2$ .

$y=f(-2)=\frac{-4}{-6+5}=4\;\;\;\;\;\;\;$ $\;\;\;\;P_T=(-2,4)$

$f´(-2)= \underset{h \to 0}{\lim}\frac{f(-2+h)-f(-2)}{h}=\underset{h \to 0}{\lim}\frac{\frac{2(-2+h)}{3(-2+h)+5}-4}{h}:\frac{\frac{2(-2+0)}{3(-2+0)+5)}-4}{0}=\frac{0}{0}:indeterminado$

$f´(-2)=\underset{h\to 0}{\lim}\frac{\frac{-4+2h}{-6+3h+5}-4}{h}=\underset{h \to 0}{\lim}\frac{\frac{(-4+2h)-4(3h-1)}{(3h-1)}}{h}=\underset{h\to 0}{\lim}\frac{-4+2h-12+4}{h(3h-1)}=\underset{h \to 0}{\lim}\frac{-10h}{h(3h-1)}=\frac{-10}{-1}=10$

Ejemplo 4.

Obtener mediante la definición de la derivada, la ecuación de la recta tangente a $f(x)=\sqrt{4-x }$ en $x = 0$.

$f(0)=\sqrt{4-x}=2\;\;\;\;\;\;\;\;\;\;\;\;\;P_T(0,2)$

$f´(0)=\underset{h \to 0}{\lim}\frac{f(0+h)-f(0)}{h}: indeterminado$

$f´(0)=\underset{h \to 0}{\lim}\frac{f(0+h)-f(0)}{h}=\underset{h \to 0}{\lim}\frac{\sqrt{4+h}-2}{h}.\frac{\sqrt{4+h}+2}{\sqrt{4+h}+2}=\underset{h \to 0}{\lim}\frac{4+h-4}{h(\sqrt{4+h}+2)}=\underset{h \to 0 }{\lim}\frac{1}{\sqrt{4+h}+2}=\frac{1}{4}$