Introducción

El principio de mínimos cuadrados establece un criterio matemático a través del cual, es posible encontrar la "mejor" línea para un conjunto de parejas de datos. La ventaja de usar un criterio matemático sobre otros métodos visuales (a ojo) es que, en estos últimos, dependemos del juicio personal del experimentador. Por mucho esmero y cuidado que se tenga, los métodos de ajuste visuales no nos dan la seguridad de la importancia cuantitativa de los datos.

A continuación haremos una explicación que nos permita entender el criterio matemático que establece el método de mínimos cuadrados para encontrar la ''mejor" recta que describa el comportamiento lineal (si es el caso) de un conjunto de parejas de datos. Supongamos que hemos registrado $N$ valores de una variable $y$ medidos como una función de otra variable $x$ . El método de mínimos cuadrados supone que la incertidumbre asociada a la variable $x$ es mucho más pequeña que la incertidumbre asociada a la variable $y$ . En otras palabras, que los valores de $x$ se conocen con una precisión mucho mayor que los de la variable $y$ .

La pregunta por contestar es: ¿cuál de todas las líneas en el plano $X-Y$ escogemos como la mejor, y que queremos decir con ''la mejor"?

Para lo anterior mostramos en la figura  los puntos que representan a nuestras $N$ parejas de datos en el plano $X-Y$ . En esta gráfica se muestra la línea $AB$ como la candidata a la ''mejor" línea. Consideremos todos los intervalos verticales entre cada punto ''experimental" y la línea. Estos intervalos estan indicados por los segmentos $P_1Q_1$ , $P_2Q_2$ , $P_3Q_3$ , etc. Se define la ''mejor" línea como aquella que minimiza la suma de los cuadrados de las longitudes de todos estos segmentos, es decir

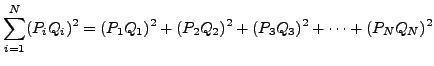$$\sum_{i=1}^N (P_iQ_i)^2=(P_1Q_1)^2+(P_2Q_2)^2+(P_3Q_3)^2+\cdots+(P_NQ_N)^2$$ (A.1)

Encontrar la ''mejor" recta que satisfaga este criterio de minimizar la cantidad anterior, significa encontrar el valor numérico de pendiente $a$ y ordenada al origen $b$ de la misma.

Si suponemos que la ecuación de la mejor recta que representa el comportamiento lineal de las $N$ parejas de datos mencionadas es:

$$y=ax+b,$$ (A.2)

entonces el tamaño del i-ésimo segmento $P_iQ_i$ es la distancia entre el valor experimental de la componente vertical $y_i$ y el valor de $y$ dado por la ecuación (A.2) cuando esta se evalua en el valor de la correspondiente coordenada $x_i$ , al cual llamaremos $y'_i$ , ésto es

$$y'_i=ax_i+b.$$ (A.3)

Así el tamaño del segmento $P_iQ_i=\vert y_i-y'_i\vert$ se obtienen en general sustituyendo $y'_i$ en términos de la ecuación anterior,

$$\delta y_i=y_i-(ax_i+b),$$ (A.4)

esta diferencias de coordenadas verticales $y_i-y'_i$ pueden ser tanto positivas como negativas dependiendo si el valor experimental de la componente vertical es más alto o más bajo que el valor que le corresponde según la ecuación de la ''mejor" recta, dada por la ecuación (A.4). En la gráfica estos casos se ven como puntos (datos experimentales) por arriba o por abajo de la ''mejor" recta. Para evitarnos problemas con los signos, construímos una cantidad $M$ como la suma de los cuadrados de las cantidades $\delta y_i$

$$M=\sum_i^N \delta y_i^2=\sum_i^N [y_i-(ax_i+b)]^2.$$ (A.5)

El criterio de mínimos cuadrados nos permite obtener los valores deseados de $a$ y $b$ a partir de minimizar la cantidad $M$ , así

$$\begin{array}{cc} \frac{\partial M}{\partial a}=0; & \frac{\partial M}{\partial b}=0. \end{array}$$ (A.6)

Si desarrollamos algebraicamente la suma de binomios que forman la cantidad $M$ de la ecuación dada por (A.11) tenemos que

$$M=\sum_i^N y_i^2 +a^2\sum_i^N x_i^2-2a\sum_i^N x_iy_i +2ab\sum_i^N x_i-2b\sum_i^N y_i+Nb^2,$$ (A.7)

al tomar las derivadas parciales de esta cantidad respecto de $a$ como de $b$ obtenemos

$$\begin{array}{ccc} & \frac{\partial M}{\partial a}= 2a\sum_{i... ...rtial b}=2a\sum_{i=1}^N x_i+2nb-2\sum_{i=1}y_i=0 &. \end{array}$$ (A.8)

Resolviendo este sistema de ecuaciones para $a$ y $b$ respectivamente se obtienen las fórmulas básicas de ajuste de pendiente $a$ y ordenada al origen $b$ de la ''mejor" recta que describe el comportamiento lineal de las $N$ parejas de datos,

$$\begin{array}{ccc} a=\frac{N\sum_{i=1}^N(x_iy_i)- \sum_{i=1}^... ..._i)}{ N \sum_{i=1}^N x_i^2-(\sum_{i=1}^N x_i)^2}& . \end{array}$$ (A.9)

De aquí en adelante las fórmulas (A.9) se aplicarán automáticamente a ajustes de parejas de datos experiemtnales que muestren una clara evidencia de comportamiento lineal.

Por completez, damos a continuación (sin hacer la deducción) las fórmulas de las incertidumbres, que el método de mínimos cuadrados, asocia tanto a la pendiente $a$ , como a la ordenada al origen $b$ ,

$$\begin{array}{ccc} \delta a=S_y \times \sqrt{\frac{N}{N \sum_... ...c{ \sum_i x_i^2 }{ N \sum_i x_i^2-(\sum_i x_i)^2} } \end{array}$$ (A.10)

donde

$$S_y=\sqrt{\frac{\sum_i (\delta y_i)^2}{N-2}},$$ (A.11)

con $\delta y_i$ dada por la ecuación (A.4). De manera que al reportar los valores numéricos de $a$ y $b$ característicos de la mejor recta, estos deben ser reportados con sus correspondietnes incertidumbres, $a\pm \delta a$ y $b \pm \delta b$ .

Por cuestiones prácticas se recomienda construír la siguiente tabla con el fin de hacer claros los cálculos y en su caso poder reproducirlos facilmente y verificar los resultados.

$i$	$x_i$	$y_i$	$x_iy_i$	$x_i^2$
$1$	$x_1$	$y_1$	$x_1y_1$	$x_1^2$
$2$	$x_2$	$y_2$	$x_2y_2$	$x_2^2$
$3$	$x_3$	$y_3$	$x_3y_3$	$x_3^2$
$\vdots$	$\vdots$	$\vdots$	$\vdots$	$\vdots$
$N$	$x_N$	$y_N$	$x_Ny_N$	$x_N^2$
	$\sum x_i$	$\sum y_i$	$\sum (x_iy_i)$	$\sum x_i^2$