Resultados
En esta sección se presentan los resultados obtenidos sobre posición promedio 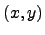 , entropía de Shannon y en
algunos casos la evolución temporal de la densidad de probabilidad de paquetes de onda en diferentes condiciones físicas. En todos
los ejemplos el paquete al tiempo
, entropía de Shannon y en
algunos casos la evolución temporal de la densidad de probabilidad de paquetes de onda en diferentes condiciones físicas. En todos
los ejemplos el paquete al tiempo 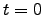 está dado por
está dado por
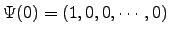 , que en representación de coordenadas espaciales
corresponde a una gaussiana localizada en el origen.
, que en representación de coordenadas espaciales
corresponde a una gaussiana localizada en el origen.
En todos los ejemplos el campo eléctrico de vias se aplica en la dirección de las 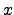 positivas, con frecuencia
positivas, con frecuencia
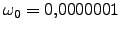 y
y 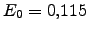 . El intervalo
de tiempo empleado en todos los casos es
. El intervalo
de tiempo empleado en todos los casos es
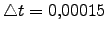 , que permite el estudio a lo largo de
, que permite el estudio a lo largo de
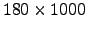 iteraciones, lo que
equivale aproximadamente a 24 oscilaciones de ciclotrón, pues
iteraciones, lo que
equivale aproximadamente a 24 oscilaciones de ciclotrón, pues
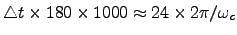 . Los ejemplos se
ejecutaron bajo dos frecuencias de ciclotrón distintas
. Los ejemplos se
ejecutaron bajo dos frecuencias de ciclotrón distintas
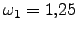 y
y
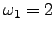 ; la primera corresponde a un estado de resistencia
cero y la segunda a un máximo de la magnetorresistencia, de acuerdo a Zudov (1). Las amplitudes de campo eléctrico de
microondas son
; la primera corresponde a un estado de resistencia
cero y la segunda a un máximo de la magnetorresistencia, de acuerdo a Zudov (1). Las amplitudes de campo eléctrico de
microondas son
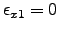 y
y
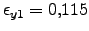 y la fase
y la fase 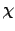 es cero. Además para todos los ejemplos
el número máximo de estados considerados fue
es cero. Además para todos los ejemplos
el número máximo de estados considerados fue
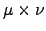
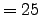 ya que
ya que 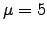 y
y 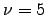 .
La correspondencia entre las cantidades físicas adimencionales empleadas y las cantidades usadas experimentalmente por (1) son: para
.
La correspondencia entre las cantidades físicas adimencionales empleadas y las cantidades usadas experimentalmente por (1) son: para
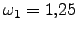 y
y 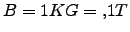 ;
;
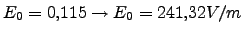 ,
,
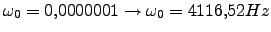 ,
,
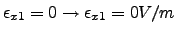 ,
,
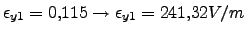 y
y
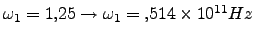 , mientras que para
, mientras que para
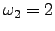 y
y
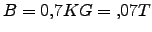 ;
se tiene
;
se tiene
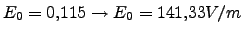 ,
,
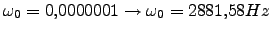 ,
,
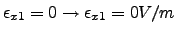 ,
,
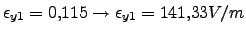 y
y
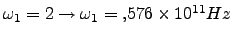 .
.
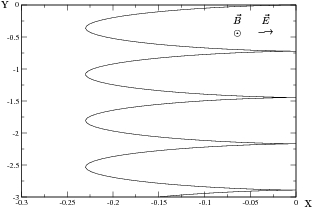
En la figura ![[*]](/usr/share/latex2html/icons/crossref.png) puede verse el movimiento de la posición promedio del paquete de ondas en ausencia de
impurezas y microondas. Se observa el movimiento de deriva en dirección perpendicular al campo eléctrico, tal como lo
predice la mecánica clásica.
puede verse el movimiento de la posición promedio del paquete de ondas en ausencia de
impurezas y microondas. Se observa el movimiento de deriva en dirección perpendicular al campo eléctrico, tal como lo
predice la mecánica clásica.
Figura:
Posición promedio 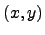 de un paquete de ondas en ausencia de impurezas y microondas.
de un paquete de ondas en ausencia de impurezas y microondas.
 |
En la gráfica ![[*]](/usr/share/latex2html/icons/crossref.png) se tiene la entropía de Shannon y la posición promedio de un paquete de ondas sin radiación de microondas.
En
se tiene la entropía de Shannon y la posición promedio de un paquete de ondas sin radiación de microondas.
En ![[*]](/usr/share/latex2html/icons/crossref.png) (a), puede verse la entropía de Shannon como función del tiempo, para un paquete de ondas en presencia de
100 impurezas con potencial de
(a), puede verse la entropía de Shannon como función del tiempo, para un paquete de ondas en presencia de
100 impurezas con potencial de 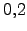 colocadas aleatoriamente en una región de
colocadas aleatoriamente en una región de
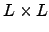 con
con 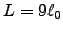 , que corresponde a una densidad de impurezas
, que corresponde a una densidad de impurezas
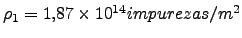 para
para
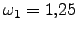 , y
, y
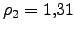 x
x
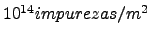 para
para
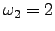 .
Recordar que
.
Recordar que 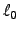 es función del campo magnético.
La gráfica
es función del campo magnético.
La gráfica ![[*]](/usr/share/latex2html/icons/crossref.png) (b) muestra el movimiento de la posición promedio del paquete. En
(b) muestra el movimiento de la posición promedio del paquete. En ![[*]](/usr/share/latex2html/icons/crossref.png) (a) la
entropía se satura para tiempos largos lo que coincide con la gran aleatoriedad de la trayectoria media del paquete de ondas. Un comportamiento
muy similar se observa cuando se introduce radiación de microondas con frecuencia
(a) la
entropía se satura para tiempos largos lo que coincide con la gran aleatoriedad de la trayectoria media del paquete de ondas. Un comportamiento
muy similar se observa cuando se introduce radiación de microondas con frecuencia
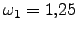 ver figura
ver figura ![[*]](/usr/share/latex2html/icons/crossref.png) , y
, y
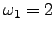 ver figura
ver figura ![[*]](/usr/share/latex2html/icons/crossref.png) .
.
En la figura ![[*]](/usr/share/latex2html/icons/crossref.png) se puede observar lo que en
se puede observar lo que en ![[*]](/usr/share/latex2html/icons/crossref.png) , pero con
, pero con
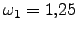 . La densidad de impurezas para generar
a
. La densidad de impurezas para generar
a ![[*]](/usr/share/latex2html/icons/crossref.png) es de 100 impurezas en un cuadro de
es de 100 impurezas en un cuadro de 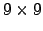 unidades, lo que corresponde a
unidades, lo que corresponde a 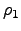 . El mismo tratamiento se aplica para
generar a la figura
. El mismo tratamiento se aplica para
generar a la figura ![[*]](/usr/share/latex2html/icons/crossref.png) , pero con
, pero con
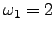 , que le corresponde como densidad de impurezas a
, que le corresponde como densidad de impurezas a 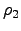 .
.
Figura:
Gráficas sin radiación externa. Densidad de impurezas, 100 impurezas en 9 unidades
cuadradas con potencial repulsivo de 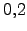 , lo que corresponde a una densidad de impurezas
, lo que corresponde a una densidad de impurezas
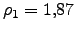 x
x
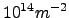 para
para
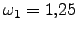 , y
, y
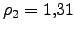 x
x
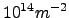 para
para
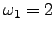 .
(a) Entropía de Shanonn
.
(a) Entropía de Shanonn 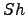 en el tiempo
en el tiempo 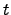 . (b) Trayectoria
. (b) Trayectoria 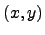 promedio del paquete a lo largo del mismo tiempo
promedio del paquete a lo largo del mismo tiempo  que en (a).
que en (a).
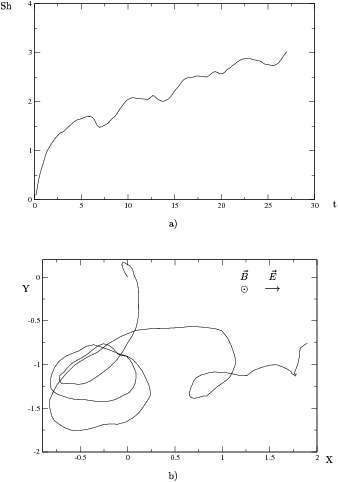 |
Figura:
Gráficas con radiación externa,
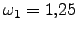 . Densidad de impurezas, 100 impurezas
en 9 unidades cuadradas con potencial repulsivo de
. Densidad de impurezas, 100 impurezas
en 9 unidades cuadradas con potencial repulsivo de 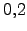 , lo que corresponde a una densidad de impurezas
, lo que corresponde a una densidad de impurezas
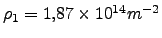 . (a) Entropía de Shanonn
. (a) Entropía de Shanonn 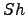 en el tiempo
en el tiempo 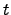 . (b)
Trayectoria
. (b)
Trayectoria 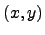 promedio del paquete a lo largo del mismo tiempo
promedio del paquete a lo largo del mismo tiempo 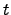 que en (a).
que en (a).
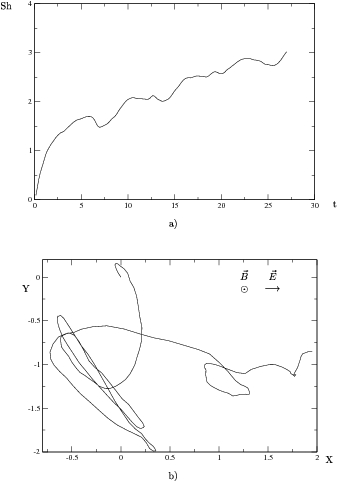 |
Figura:
Gráficas con radiación externa,
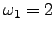 . Densidad de impurezas, 100 impurezas en
9 unidades cuadradas con potencial repulsivo de
. Densidad de impurezas, 100 impurezas en
9 unidades cuadradas con potencial repulsivo de 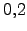 , lo que corresponde a una densidad de impurezas
, lo que corresponde a una densidad de impurezas
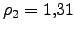 x
x
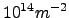 . (a) Entropía de Shanonn
. (a) Entropía de Shanonn 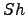 en el tiempo
en el tiempo 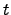 . (b)
Trayectoria
. (b)
Trayectoria 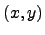 promedio del paquete a lo largo del mismo tiempo
promedio del paquete a lo largo del mismo tiempo 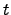 que en (a).
que en (a).
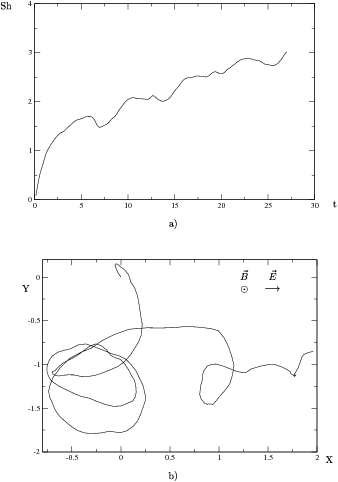 |
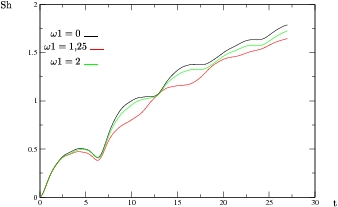
Figura:
Gráfica que muestra una comparación en las entropías de Shannon vs. t, para los distintos valores de
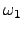 , notando una diferencia entre la entropía de
, notando una diferencia entre la entropía de
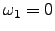 y
y
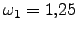 , así como entre
, así como entre
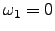 y
y
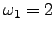 .
.
 |
En la figura ![[*]](/usr/share/latex2html/icons/crossref.png) se muestra la entropía de Shannon y la posición promedio de un paquete de ondas sin radiación de microondas.
En la figura
se muestra la entropía de Shannon y la posición promedio de un paquete de ondas sin radiación de microondas.
En la figura ![[*]](/usr/share/latex2html/icons/crossref.png) (a) se observa la entropía de Shannon en función del tiempo para un paquete de ondas en presencia de 10
impurezas con potencial de
(a) se observa la entropía de Shannon en función del tiempo para un paquete de ondas en presencia de 10
impurezas con potencial de 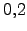 colocadas aleatoriamente en un cuadro de
colocadas aleatoriamente en un cuadro de 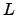 x
x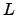 con
con 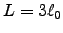 , lo que corresponde a una densidad
, lo que corresponde a una densidad
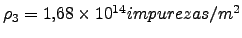 para
para
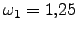 , y
, y
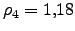 x
x
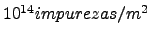 para
para 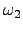 .
La figura
.
La figura ![[*]](/usr/share/latex2html/icons/crossref.png) (b) muestra la trayectoria promedio del paquete, mientras que en la figura
(b) muestra la trayectoria promedio del paquete, mientras que en la figura ![[*]](/usr/share/latex2html/icons/crossref.png) se observa la densidad
de probabilidad
se observa la densidad
de probabilidad
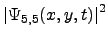 en 3D. Mientras que para generar a la figura
en 3D. Mientras que para generar a la figura ![[*]](/usr/share/latex2html/icons/crossref.png) se aplica
se aplica
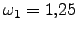 y
y 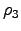 en tanto para
en tanto para ![[*]](/usr/share/latex2html/icons/crossref.png) se utiliza
se utiliza
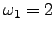 y
y 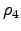 . Al ver la entropía de
. Al ver la entropía de ![[*]](/usr/share/latex2html/icons/crossref.png) (a) y
(a) y ![[*]](/usr/share/latex2html/icons/crossref.png) (a) y
contrastarlas con las de
(a) y
contrastarlas con las de ![[*]](/usr/share/latex2html/icons/crossref.png) (a) y
(a) y ![[*]](/usr/share/latex2html/icons/crossref.png) (a) respectivamente, notamos que estos dos últimos sistemas son más entrópicos
lo que concuerda con que
(a) respectivamente, notamos que estos dos últimos sistemas son más entrópicos
lo que concuerda con que
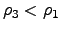 y
y
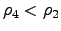 . Al hacer un análisis cualitativo entre
. Al hacer un análisis cualitativo entre ![[*]](/usr/share/latex2html/icons/crossref.png) (a) con
(a) con ![[*]](/usr/share/latex2html/icons/crossref.png) (a) y
(a) y
![[*]](/usr/share/latex2html/icons/crossref.png) (a) con
(a) con ![[*]](/usr/share/latex2html/icons/crossref.png) (a), ver figura
(a), ver figura ![[*]](/usr/share/latex2html/icons/crossref.png) , notamos una diferencia entre las entropías, pero al comparar
las entropías de
, notamos una diferencia entre las entropías, pero al comparar
las entropías de ![[*]](/usr/share/latex2html/icons/crossref.png) (a) con
(a) con ![[*]](/usr/share/latex2html/icons/crossref.png) (a) y
(a) y ![[*]](/usr/share/latex2html/icons/crossref.png) (a), no observamos una diferencia. Las figuras
(a), no observamos una diferencia. Las figuras ![[*]](/usr/share/latex2html/icons/crossref.png) y
y
![[*]](/usr/share/latex2html/icons/crossref.png) muestran la densidad de probabilidad
muestran la densidad de probabilidad
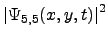 en 3D para los casos de la figuras
en 3D para los casos de la figuras
![[*]](/usr/share/latex2html/icons/crossref.png) y
y ![[*]](/usr/share/latex2html/icons/crossref.png) respectivamente, en distintos instantes
respectivamente, en distintos instantes 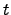 .
.
Otra prueba interesante es colocar impurezas con potenciales negativos. En la figura ![[*]](/usr/share/latex2html/icons/crossref.png) , observamos la entropía de Shannon y la
trayectoria promedio de un paquete de ondas en ausencia de microondas, y con una densidad de impurezas
, observamos la entropía de Shannon y la
trayectoria promedio de un paquete de ondas en ausencia de microondas, y con una densidad de impurezas 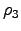 para
para
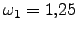 , y
, y
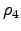 para
para
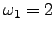 , pero con un valor de potencial de
, pero con un valor de potencial de 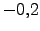 para cada una. Las figuras
para cada una. Las figuras ![[*]](/usr/share/latex2html/icons/crossref.png) y
y ![[*]](/usr/share/latex2html/icons/crossref.png) se generaron
bajo las mismas condiciones que
se generaron
bajo las mismas condiciones que ![[*]](/usr/share/latex2html/icons/crossref.png) , pero
, pero ![[*]](/usr/share/latex2html/icons/crossref.png) con
con
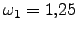 y
y 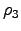 , mientras que
, mientras que ![[*]](/usr/share/latex2html/icons/crossref.png) se calculó con
se calculó con
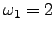 y
y 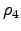 . Haciendo un análisis cualitativo, se puede observar que
. Haciendo un análisis cualitativo, se puede observar que ![[*]](/usr/share/latex2html/icons/crossref.png) (a) muestra una entropía mayor respecto
de
(a) muestra una entropía mayor respecto
de ![[*]](/usr/share/latex2html/icons/crossref.png) (a), esto para tiempos
(a), esto para tiempos
![$ t\in [5,20]$](img80.png) lo que corresponde a un tiempo
lo que corresponde a un tiempo
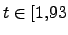 x
x
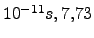 x
x
![$ 10^{-11}s]$](img83.png) .
Un comportamiento similar se observa entre
.
Un comportamiento similar se observa entre ![[*]](/usr/share/latex2html/icons/crossref.png) (a) y
(a) y ![[*]](/usr/share/latex2html/icons/crossref.png) (a).
(a).
Otro punto a notar es que los rizos de ![[*]](/usr/share/latex2html/icons/crossref.png) (b) y
(b) y ![[*]](/usr/share/latex2html/icons/crossref.png) (b) son más pequeños respecto de los de
(b) son más pequeños respecto de los de ![[*]](/usr/share/latex2html/icons/crossref.png) (b) y
(b) y
![[*]](/usr/share/latex2html/icons/crossref.png) (b).
(b).
Figura:
Gráficas sin radiación externa. Densidad de impurezas, 10 impurezas en 9 unidades
cuadradas con potencial repulsivo de 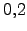 , lo que corresponde a una densidad de impurezas
, lo que corresponde a una densidad de impurezas
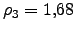 x
x
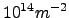 para
para
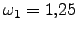 , y
, y
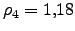 x
x
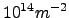 para
para
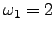 .
(a) Entropía de Shanonn
.
(a) Entropía de Shanonn 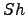 en el tiempo
en el tiempo 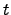 . (b)
Trayectoria
. (b)
Trayectoria 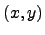 promedio del paquete a lo largo del mismo tiempo
promedio del paquete a lo largo del mismo tiempo 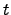 que en (a).
que en (a).
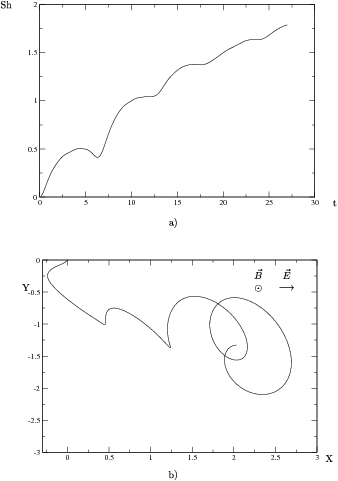 |
Figura:
Figura que nos muestra la evolución temporal de
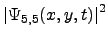 ,
con
,
con
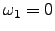 , campo eléctrico de vias
, campo eléctrico de vias
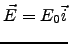 y campo magnético
y campo magnético
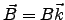 , en un medio con
densidad de impurezas
, en un medio con
densidad de impurezas 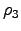 para
para
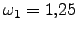 , y
, y 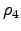 para
para
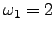 .
.
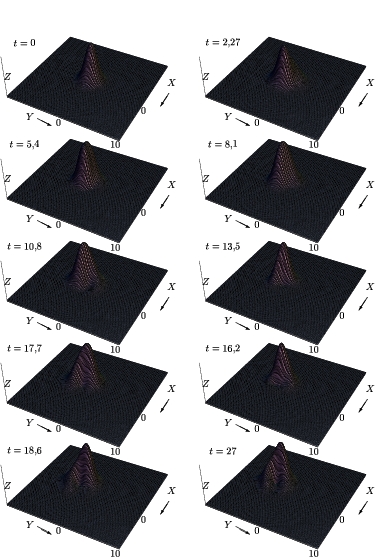 |
Figura:
Gráficas con radiación externa
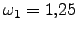 . Densidad de impurezas, 10 impurezas
en 9 unidades cuadradas con potencial repulsivo de
. Densidad de impurezas, 10 impurezas
en 9 unidades cuadradas con potencial repulsivo de 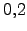 , lo que corresponde a una densidad de impurezas
, lo que corresponde a una densidad de impurezas
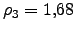 x
x
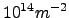 .
(a) Entropía de Shanonn
.
(a) Entropía de Shanonn 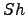 en el tiempo
en el tiempo 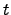 . (b)
Trayectoria
. (b)
Trayectoria 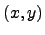 promedio del paquete a lo largo del mismo tiempo
promedio del paquete a lo largo del mismo tiempo 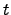 que en (a).
que en (a).
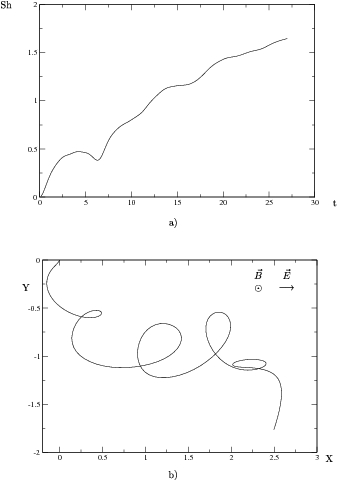 |
Figura:
Gráficas con radiación externa
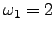 . Densidad de impurezas,10 impurezas en 9
unidades cuadradas con potencial repulsivo de
. Densidad de impurezas,10 impurezas en 9
unidades cuadradas con potencial repulsivo de 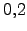 , lo que corresponde a una densidad de impurezas
, lo que corresponde a una densidad de impurezas
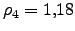 x
x
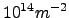 .
(a) Entropía de Shanonn
.
(a) Entropía de Shanonn 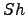 en el tiempo
en el tiempo 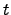 . (b)
Trayectoria
. (b)
Trayectoria 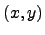 promedio del paquete a lo largo del mismo tiempo
promedio del paquete a lo largo del mismo tiempo 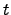 que en (a).
que en (a).
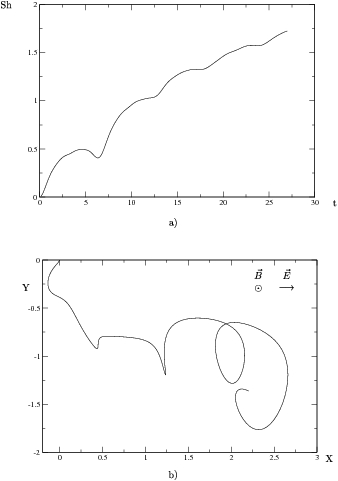 |
Figura:
Figura que nos muestra la evolución temporal de
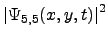 ,
con
,
con
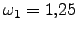 , campo eléctrico de vias
, campo eléctrico de vias
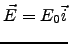 y campo magnético
y campo magnético
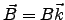 , en un medio con
densidad de impurezas
, en un medio con
densidad de impurezas 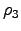 .
.
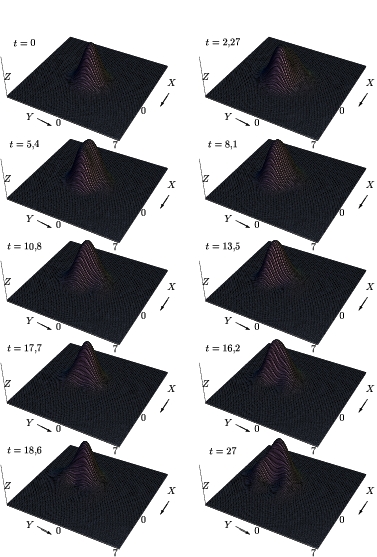 |
Figura:
Figura que nos muestra la evolución temporal de
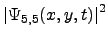 ,
con
,
con
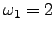 , campo eléctrico de vias
, campo eléctrico de vias
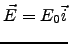 y campo magnético
y campo magnético
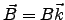 , en un medio con
densidad de impurezas
, en un medio con
densidad de impurezas 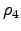 .
.
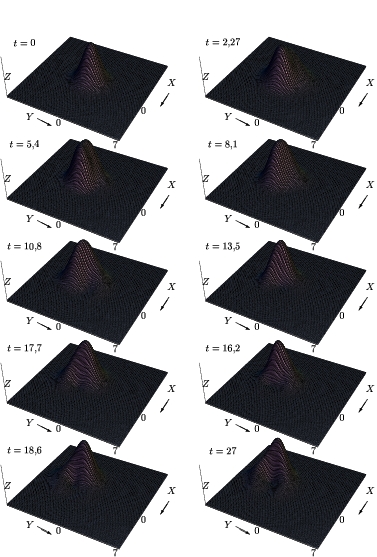 |
Figura:
Gráficas sin radiación externa. Densidad de impurezas, 10 impurezas
con potencial atractivo de 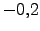 en
en 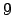 unidades cuadradas, lo que corresponde a una densidad de impurezas
unidades cuadradas, lo que corresponde a una densidad de impurezas 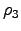 para
para
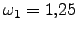 y
y
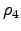 para
para
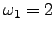 .
(a) Entropía de Shanonn
.
(a) Entropía de Shanonn 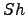 en el tiempo
en el tiempo 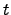 .
(b) Trayectoria
.
(b) Trayectoria 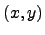 promedio del paquete a lo largo del mismo tiempo
promedio del paquete a lo largo del mismo tiempo 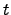 que en (a).
que en (a).
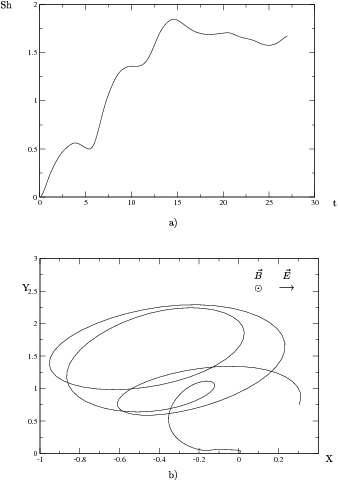 |
Figura:
Gráficas con radiación externa
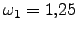 . Densidad de impurezas, 10 impurezas
con potencial atractivo de
. Densidad de impurezas, 10 impurezas
con potencial atractivo de 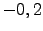 en 9 unidades cuadradas, lo que corresponde a una densidad de impurezas
en 9 unidades cuadradas, lo que corresponde a una densidad de impurezas
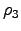 . (a) Entropía de Shanonn
. (a) Entropía de Shanonn 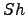 en el timempo
en el timempo 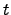 . (b)
Trayectoria
. (b)
Trayectoria 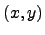 promedio del paquete a lo largo del mismo tiempo
promedio del paquete a lo largo del mismo tiempo 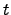 que en (a).
que en (a).
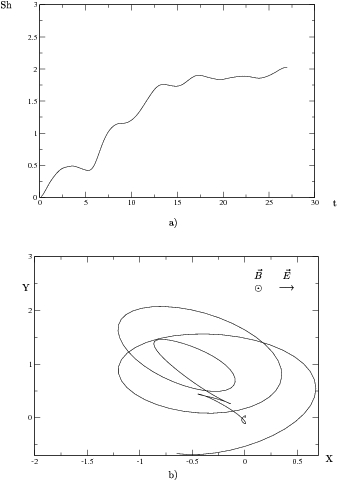 |
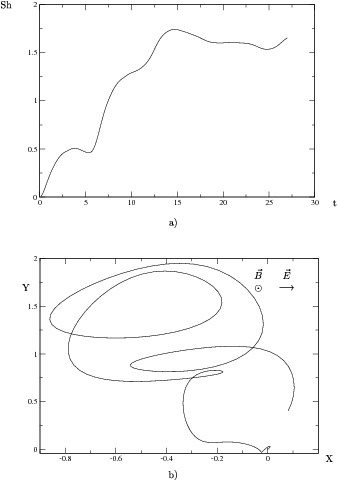
Figura:
Gráficas con radiación externa
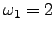 . Densidad de impurezas,10 impurezas con potencial atractivo de
. Densidad de impurezas,10 impurezas con potencial atractivo de 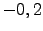 en 9 unidades cuadradas, lo que corresponde a una densidad de impurezas
en 9 unidades cuadradas, lo que corresponde a una densidad de impurezas 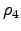 .
(a) Entropía de Shanonn
.
(a) Entropía de Shanonn 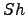 en el tiempo
en el tiempo 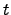 . (b)
Trayectoria
. (b)
Trayectoria 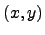 promedio del paquete a lo largo del mismo tiempo
promedio del paquete a lo largo del mismo tiempo 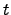 que en (a).
que en (a).
 |
2006-02-20










