Problema 1: La curva D es
una curva que se define recursivamente de la siguiente manera: La
curva D de nivel 0 es simplemente un segmento de recta. Para toda N
> 0, la curva D de nivel N se obtiene de la curva D de nivel N-1
reemplazando de manera alternada (una vez por la izquierda y una vez
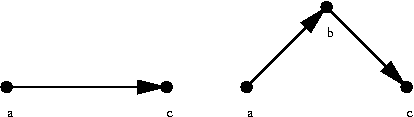
por la derecha) cada segmento ac
de recta por dos segmentos ab
y bc de recta de la siguiente
manera:

Suponga que se definen las ocho direcciones E, NE, N, NO, O,
SO, S y SE como los números 0, 1, 2, 3, 4, 5, 6 y 7 y que la
curva D de nivel 0 es un segmento E. Diseña un algoritmo
recursivo para encontrar la sucesión de direcciones que definen
la curva D de nivel N. Por ejemplo, si N = 2 las direcciones
serían N, E, S y E. Escribe un programa llamado curvadZZ (donde ZZ es una clave de dos
dígitos asignada por el profesor) basado en tu algoritmo
que acepte como entrada un entero N y que escriba como salida la
sucesión de números correspondiente a la curva D de nivel
N. Puedes suponer que 0 <= N <= 100.
| Ejemplo de entrada |
Ejemplo de salida |
| 2 |
2 0 6 0 |
Problema 2: Sea n un entero positivo y sea a[1], a[2], ..., a[n] un arreglo de enteros distintos ordenados ascendentemente, es decir, con a[1] < a[2] < ... < a[n]. El problema del punto fijo es el de encontrar algún entero k tal que a[k] = k o decidir que ese entero no existe. Como un ejemplo, si el arreglo fuera -3, -1, 1, 4, 5, 9 entonces cualquiera de k = 4 o k = 5 sería una respuesta correcta, pero si el arreglo fuera -3, 1, 4, 5, 9 entonces k no existe. Escribe un programa llamado pfijoZZ (donde ZZ es la clave de dos dígitos asignada por el profesor) basado en un algoritmo de divide y vencerás para resolver el problema del punto fijo (que es similar al de la búsqueda binaria). Tu programa debe leer un entero N y un vector A = (A1, A2, ..., AN) con N enteros positivos tales que A1 < A2 < ... < AN y debe escribir dos enteros M y P, donde M = AM y P es el número de preguntas que se hicieron para encontrar M. Por ejemplo si N = 5 y A = (1, 2, 4, 8, 16) entonces tu algoritmo debe preguntar primero en la posición 3 y después preguntará en la posición 1, encontrando un 1 y terminando. Puedes suponer que 1 <= N <= 1,000,000 y que 0 < A1 < A2 < ... < AN < 1,000,000,000. También puedes suponer que siempre habrá al menos un punto fijo.
| Ejemplo de entrada |
Ejemplo de salida |
| 5 1 2 4 8 16 |
1 2 |
Notas: Tus programas no deben leer ni escribir nada adicional a lo que se indica en el enunciado. El tiempo de ejecución de sus algoritmos será considerado como parte de la evaluación.