Para este caso particular de movimiento uniformemente acelerado,
la ecuación (5.5) toma la forma
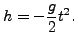 |
(6.6) |
Podemos tomar dos caminos distintos.
En el primero, hacemos una regresión no lineal directamente con
la ec. (5.6) como se indica en el apéndice B. En la
figura ![[*]](/usr/share/latex2html/icons/crossref.png) pueden verse los puntos experimentales
y la regresión no lineal que es la linea continua. El resultado de la regresión
no lineal es
pueden verse los puntos experimentales
y la regresión no lineal que es la linea continua. El resultado de la regresión
no lineal es
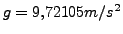 .
.
Tabla 5.2:
Tiempo al cuadrado 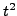 vs. altura
vs. altura 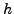 .
.
| n |
![$ t^2 \left[s^2\right]$](img21.png)
|
![$ h \left[m\right]$](img15.png)
|
| 1 |
0.2982 |
1.45 |
| 2 |
0.2876 |
1.40 |
| 3 |
0.2778 |
1.35 |
| 4 |
0.2668 |
1.30 |
| 5 |
0.2572 |
1.25 |
| 6 |
0.2476 |
1.20 |
| 7 |
0.2380 |
1.15 |
| 8 |
0.2269 |
1.10 |
| 9 |
0.2158 |
1.05 |
| 10 |
0.2044 |
1.00 |
|
En el segundo, linearizamos los datos
haciendo
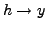 y
y
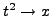 de tal manera que para el modelo
lineal
de tal manera que para el modelo
lineal
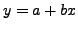 |
(6.7) |
la pendiente 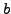 corresponde a
corresponde a 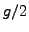 de la ecuación (5.6) y
de la ecuación (5.6) y
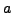 debe ser cero o por lo menos, su valor absoluto debe ser muy pequeño
comparado con el menor valor de
debe ser cero o por lo menos, su valor absoluto debe ser muy pequeño
comparado con el menor valor de 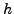 . Estos cálculos pueden verse
en la tabla 5.2.
. Estos cálculos pueden verse
en la tabla 5.2.
En la gráfica ![[*]](/usr/share/latex2html/icons/crossref.png) puede verse a
puede verse a 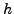 como función de
como función de 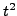 .
Si hacemos una regresión lineal con estos datos como se explica en el
apéndice A obtendremos que
.
Si hacemos una regresión lineal con estos datos como se explica en el
apéndice A obtendremos que
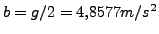 y
y
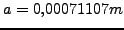 con lo que la gravedad queda dada por
con lo que la gravedad queda dada por
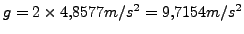 . Es
importante notar que
. Es
importante notar que 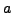 debe ser un número pequeño comparado con
debe ser un número pequeño comparado con 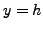 . En
este caso se cumple esta condición.
. En
este caso se cumple esta condición.
Alejandro Kunold
2006-07-03
![]() y
y
![]() de tal manera que para el modelo
lineal
de tal manera que para el modelo
lineal
![]() puede verse a
puede verse a ![]() como función de
como función de ![]() .
Si hacemos una regresión lineal con estos datos como se explica en el
apéndice A obtendremos que
.
Si hacemos una regresión lineal con estos datos como se explica en el
apéndice A obtendremos que
![]() y
y
![]() con lo que la gravedad queda dada por
con lo que la gravedad queda dada por
![]() . Es
importante notar que
. Es
importante notar que ![]() debe ser un número pequeño comparado con
debe ser un número pequeño comparado con ![]() . En
este caso se cumple esta condición.
. En
este caso se cumple esta condición.