Tema 1.
Resumen para el Tema 1.
\documentclass[12pt]{article}
%\usepackage{amssymb}
%\usepackage{amsmath}
%\usepackage{url}
%\usepackage[letterpaper,top=1.5cm,bottom=1.5cm,left=2.5cm,right=2.5cm,marginparwidth=1.75cm]{geometry}
%\usepackage{color}
%\usepackage{xcolor}
%\usepackage{enumitem}
%\usepackage{mtpro2}
\usepackage{comment, multicol}
\usepackage{calc,pict2e,picture}
%\usepackage{textgreek,textcomp,gensymb,stix}
\usepackage{amssymb}
\usepackage{hyperref}
\usepackage{amsmath}
\begin{document}
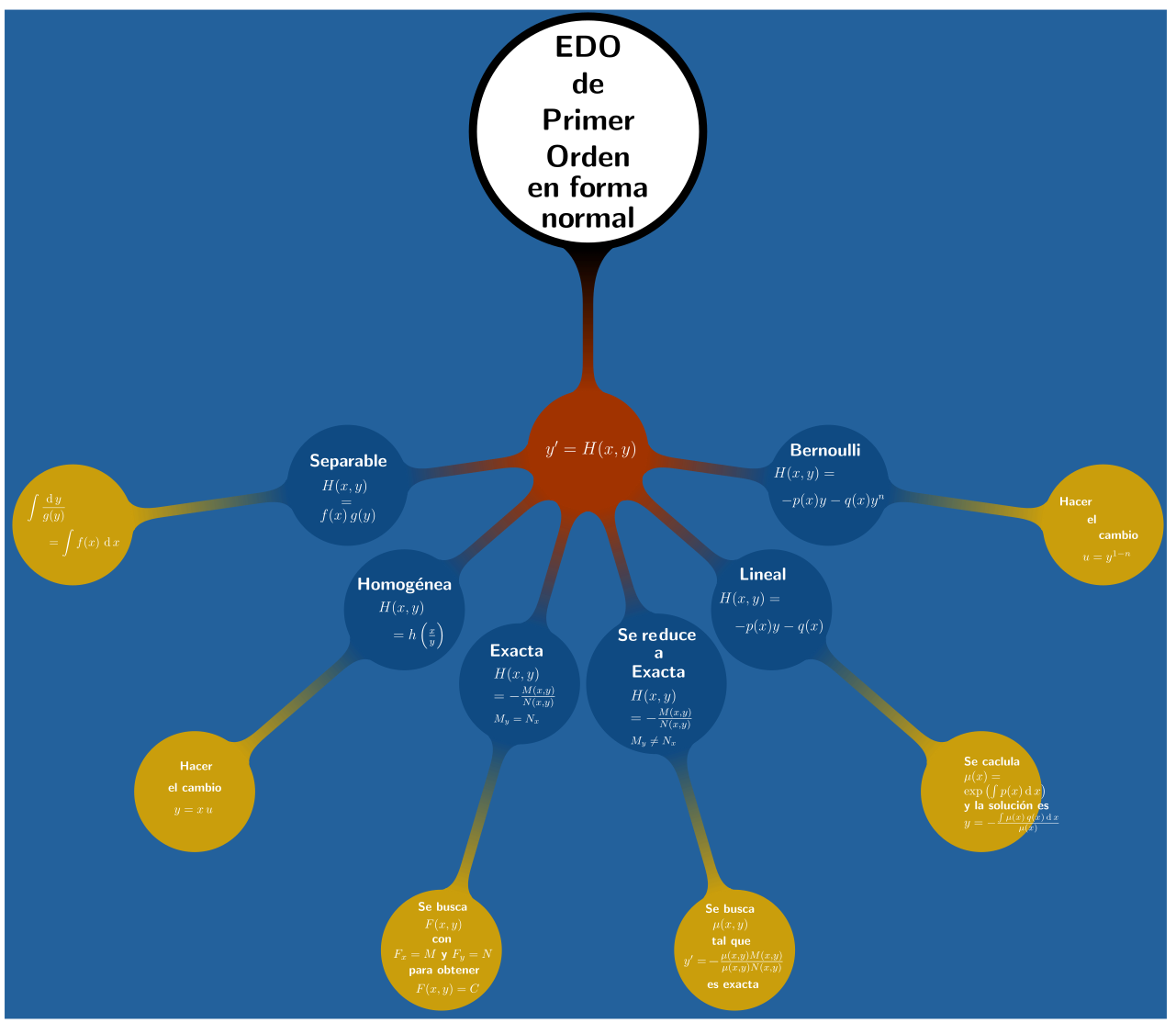
\section*{Ecuaciones Diferenciales Ordinarias de Primer Orden (parte I)}
Denotemos por $\mathbb{R}$, al conjunto de los números reales. En lo subsecuente,
consideraremos que $y$ es una función diferenciable en algún intervalo aberto $I$ de
$\mathbb R$ y que depende de la variable $x$.
Es decir, $y: I\to \mathbb{R}$ tal que $y=y(x)$ y tal que $y^\prime:I^*\to\mathbb{R}$ existe para algún $I^*\subset I$.
\emph{{Forma general de una Ecuación Diferencial Ordinaria de Primer Orden}}:
$$
F(x,y,y^\prime)=0
$$
donde $F$ es una función que relaciona las variables $x$, $y$ e $y^\prime$.
\emph{ Forma normal de una Ecuación Diferencial Ordinaria de Primer Orden (EDO)}:
$$
y^\prime=H(x,y)
$$
donde $H$ es una función que relaciona las variables $x$ e $y$.\\
\emph{Teorema:}
Toda ecuación diferencial ordinaria de primer orden en forma normal puede escribirse en la forma general.\\
\emph{Solución de una ecuación diferencial ordinaria de primer orden}: Una función diferenciable $\phi(x)$ que satisface
$$F(x,\phi(x),\phi^\prime(x))=0$$
se dice \emph{solución de la Ecuación Diferencial Ordinaria}. Similarmente, una función diferenciable $\phi(x)$ que satisface
$$\phi^\prime(x)=H(x,\phi(x))$$
se llama \emph{solución de la Ecuación Diferencial Ordinaria}.
\section{Ecuaciones Diferenciales Ordinarias de Primer Orden en Forma Normal}\label{eq:normal}
Una \emph{EDO de primer orden en forma normal} tiene la forma:
$$
y^\prime=H(x,y)$$
donde $H$ es una función que relaciona a $x$ e $y$. En esta sección trataremos algunos casos.\\
En lo posterior, a una \emph{EDO de primer orden en forma normal} le diremos simplemente \emph{EDO}.
\subsection{EDO de primer orden de tipo \emph{separable}}\label{eq:separable}
Si en la EDO \ref{eq:normal}, la función
$${H(x,y)=f(x)\,g(y)},$$
se tiene una EDO de primer orden de tipo \emph{separable}. Es decir,
$$
y^\prime=f(x)\,g(y)
$$
\subsubsection{Método para resolver una EDO de primer orden de tipo \emph{separable}}\label{eq:solseparable}
\begin{enumerate}
\item Separar las variables para obtener
$$
\frac{y^\prime}{g(y)}=f(x)
$$
\item Como $y$ e $y^\prime$ son funciones de $x$, integramos con respecto de $x$ en ambos lado de la igualdad,
$$
\int\frac{y^\prime}{g(y)}\,\mathrm{d}x=\int f(x)\,\mathrm{d}x
$$
\item Usamos el cambio de variable en la parte izquierda de la igualdad (es decir, $y^\prime\,\mathrm{d}x=\,\mathrm{d}y$),
$$
\int\frac{\,\mathrm{d}y}{g(y)}=\int f(x)\,\mathrm{d}x
$$
\item Después de integrar obtenemos la \emph{solución general en forma implícita}:
$$
G(y)=F(x)+C
$$
donde $F$ y $G$ son funcioneDos diferenciables que satisfacen
$$\frac{\,\mathrm{d}\,}{\,\mathrm{d}\,y}G(y)=\frac{1}{g(y)}\quad y\quad \frac{\,\mathrm{d}\,}{\,\mathrm{d}\, x}F(x)=f(x)$$
y $C$ es la combinación de las constantes de integración de la parte derecha e izquierda.
\item Resolver, si es posible, para la variable $y$ para encontrar la forma explícita de la solución.
\item Buscamos soluciones \emph{singulares}, es decir soluciones $\phi(x)=k$ donde $k\in\mathbb{R}$.
\end{enumerate}
\fbox{\href{https://youtu.be/68WYLC5EZoA}{Video}}\\
\fbox{\href{https://youtu.be/5B2oRGQbFNU}{Ejemplo resuelto 1}}\\
\fbox{\href{https://youtu.be/Ibj0Kx4vUbQ}{Ejemplo resuelto 2}}\\
\fbox{\href{https://youtu.be/LxzxOQsmV8A}{Ejemplo resuelto 3}}\\
\fbox{\href{https://youtu.be/WYdDT7gPqXI}{Ejemplo resuelto 4}}\\
\fbox{\href{https://youtu.be/sU2vDnqw34Y}{Ejemplo resuelto 5}}
\subsection{EDO de primer orden de tipo \emph{ homogénea}}\label{eq:homogenea}
Una EDO \ref{eq:normal} se dice de tipo \emph{homogénea} si
{$$\displaystyle H(x,y)=h\Big(\frac{y}{x}\Big)$$ }
donde $h$ es una función continua. Es decir,
$$
y^\prime=h\left(\frac{y}{x}\right)
$$
\subsubsection{Método para resolver una EDO de primer orden de tipo \emph{homogénea}}
\begin{enumerate}
\item Se considera el cambio de variable $\displaystyle u=\frac{y}{x}$. Equivalentemente, se tiene $y=ux$ y de donde
$y'=u+xu'$.
\item Se sustituyen en la EDO los cambios anteriores y se obtiene la ecuaci\'on:
$$
u'=\frac{h(u)-u}{x}
$$
\item La EDO resultante es de tipo \emph{separable} en las variables $x$ y $u$. Por tanto se resuelve aplicando el método para ecuaciones \emph{separables} \ref{eq:solseparable}.
\item A la solución obtenida en el paso anterior, se aplica el cambio de variable $\displaystyle u=\frac{y}{x}$ y se simplifica.
\item Se consideran las soluciones \emph{singulares}.
\end{enumerate}
\fbox{\href{https://youtu.be/TBtvSTmSEPs}{Video}}\\
\fbox{\href{https://youtu.be/DTKsoZQx4DQ}{Ejemplo resuelto 1}}\\
\fbox{\href{https://youtu.be/Ooa-g1eDTuQ}{Ejemplo resuelto 2}}\\
\fbox{\href{https://youtu.be/9z_lJG9bmz4}{Ejemplo resuelto 3}}\\
\fbox{\href{https://youtu.be/DpXLiGmPr5Y }{Ejemplo resuelto 4}}\\
\fbox{\href{https://youtu.be/LCa1nDSo8tY}{Ejemplo resuelto 5}}\\
\fbox{\href{https://youtu.be/8gjhErhmdfo}{Ejemplo resuelto 6}}
\emph{Observación:} También se puede utilizar el cambio $\displaystyle u=\frac{x}{y}$.
\subsection{EDO de primer orden \emph{que se reducen a tipo separable}}\label{eq:tiposeparable}
Si en la EDO \ref{eq:normal}, la función
$$H(x,y)=f(ax+by+c),$$
donde $a,b,c\in \mathbb R$ se tiene una EDO de primer orden de tipo que se reduce a una \emph{separable}. Es decir,
$$
y^\prime=f(ax+by+c)
$$
\subsubsection{Método para resolver una EDO de primer orden que se reducen al tipo \emph{separable}}
Supongamos que la constante $b$ no es nula.
\begin{enumerate}
\item Consideramos el cambio de variable $z=ax+by+c$, de donde $z^\prime=a+by^\prime$ y por tanto
$$\displaystyle y^\prime=\frac{z^\prime-a}{b}.$$
\item Sustituimos en la EDO original para obtener la ecuación:
$$
\frac{z^\prime-a}{b}=f(z),
$$
que puede verse como:
$$
{z^\prime}=b\,f(z)+a
$$
que es una \emph{EDO de primer orden de tipo separable}.
\item Usamos el método para resolver las EDO de tipo separable \ref{eq:solseparable} y escribimos la solución regresando el cambio de variable.
\end{enumerate}
\subsection{EDO de primer orden \emph{ que se reduce al tipo homogénea}}\label{eq:tipohomogenea}
Una EDO \ref{eq:normal} es de tipo \emph{cuasi-homogénea} si
$$\displaystyle H(x,y)=\frac{ax+by+c}{dx+ey+f},$$
donde $a,b,c,d,e,f\in\mathbb R$. Es decir,
$$
y^\prime=\frac{ax+by+c}{dx+ey+f}
$$
Observemos que la EDO es homogénea si $c=f=0$.
\subsubsection{Método para resolver una EDO de primer orden que se reduce al tipo homogénea}
\begin{enumerate}
\item Se buscan constantes $h$ y $k$ de manera que satisfagan el sistema de ecuaciones
$$
\begin{cases}
ah+bk+c=0\\
dh+ek+f=0
\end{cases}
$$
\item Se considera el cambio de variables $\displaystyle x=X+h$ y $y=Y+k$. De aquí que $Y^\prime=y^\prime$.
\item Haciendo los cambios se obtiene la EDO de tipo homogénea
$$
Y^\prime=\frac{aX+bY}{dX+eY}
$$
\item La EDO anterior es de tipo \emph{homogénea} y por tanto se resuelve aplicando el método
para resolver una EDO de primer orden de tipo homogénea.
\item A la solución obtenida en el paso anterior se regresa el cambio de variable.
\end{enumerate}
\emph{Observación}:
Para que el método pueda aplicarse, se requiere que
$$
\left|\begin{matrix}
a&b\\
d&e
\end{matrix}\right|
$$
sea diferente de cero.\\
\fbox{\href{https://youtu.be/sVJsm4vkPuo}{Video}}\\
\fbox{\href{https://youtu.be/kuiZQXSNWBA}{Ejemplo resuelto 1}}\\
\fbox{\href{https://youtu.be/yfbC4sr7218}{Ejemplo resuelto 2}}%\\
%\fbox{\href{}{Ejemplo resuelto 3}}\\
%\fbox{\href{}{Ejemplo resuelto 4}}\\
%\fbox{\href{}{Ejemplo resuelto 5}}
\subsection{EDO de primer orden de tipo \emph{exacta}}\label{eq:exactas}
Una EDO \ref{eq:normal} es de tipo \emph{exacta} si
$$\displaystyle H(x,y)=-\frac{M(x,y)}{N(x,y)},$$
donde $M,N $ son funciones diferenciables que satisfacen
$\displaystyle\frac{\partial M(x,y)}{\partial y}=\frac{\partial N(x,y)}{\partial x}$. Es decir,
$$
y^\prime=-\frac{M(x,y)}{N(x,y)}
$$
donde
$$\frac{\partial M(x,y)}{\partial y}=\frac{\partial N(x,y)}{\partial x}.$$
\subsubsection{Método para resolver una EDO de primer orden de tipo \emph{exacta}}\label{eq:solexacta}
\begin{enumerate}
\item Nos concentramos en buscar una solución general dada en forma impícita $F(x,y)=C$ donde
$C\in\mathbb R$ es constante que satisfaga:
$$
\frac{\partial F(x,y)}{\partial x}=M(x,y)
$$
y
$$
\frac{\partial F(x,y)}{\partial y}=N(x,y)
$$
\item De integrar con respecto a $x$ la primer ecuación, proponemos
$$
F(x,y)=\int M(x,y)\,\,\,\mathrm{d}\, x =R(x,y)+k(y)
$$
\item Hallamos la función $k(y)$ tomando en cuenta la segunda ecuación.
\item Escribimos $F(x,y)=C$ donde la cons\-tan\-te $C$ agrupa las constantes obtenidas de los procesos de integración.
\end{enumerate}
\fbox{\href{https://youtu.be/cyXw1Riq-ok}{Video}}\\
\fbox{\href{https://youtu.be/Zm869G4CArI}{Ejemplo resuelto 1}}\\
\fbox{\href{https://youtu.be/r5ZAjR3rwds}{Ejemplo resuelto 2}}\\
\fbox{\href{https://youtu.be/pJwNzGwwDRg}{Ejemplo resuelto 3}}\\
\fbox{\href{https://youtu.be/uMbuUjcxwj8}{Ejemplo resuelto 4}}\\
\fbox{\href{https://youtu.be/tHzhjmv_igs}{Ejemplo resuelto 5}}
\subsection{EDO de primer orden \emph{ que se reduce a una de tipo exacta}}\label{eq:facint}
Una EDO \ref{eq:normal} se dice que se \emph{reduce a exacta mediante un factor integrante} si
$$\displaystyle H(x,y)=-\frac{M(x,y)}{N(x,y)},$$
donde $M,N $ son funciones diferenciables tales que
$\displaystyle\frac{\partial M(x,y)}{\partial y}$ es \emph{diferente} de $\displaystyle\frac{\partial N(x,y)}{\partial x}$. Es decir,
$$
y^\prime=-\frac{M(x,y)}{N(x,y)}
$$
donde
$$\frac{\partial M(x,y)}{\partial y}\neq\frac{\partial N(x,y)}{\partial x}.$$
\subsubsection{Método para resolver una EDO de primer orden \emph{ que se reduce a una de tipo exacta}}\label{eq:solfacint}
\begin{enumerate}
\item Se busca una función $\mu(x,y)$ llamada \emph{factor integrante} tal que
$$\frac{\partial}{\partial y} \mu(x,y)M(x,y)=\frac{\partial }{\partial x} \mu(x,y)N(x,y).$$
Es decir, la ecuación ,
$$
y^\prime=-\frac{\mu(x,y)M(x,y)}{\mu(x,y)N(x,y)}
$$
es una EDO de tipo \emph{exacta}.
\item Algunos factores integrantes pueden encontrarse mediante las siguientes \emph{recetas}:
\begin{itemize}
\item Si $\displaystyle \frac{\displaystyle\frac{\partial}{\partial y} M(x,y)-\frac{\partial }{\partial x} N(x,y)}{N(x,y)}=h(x)$
entonces $\mu(x,y)=\mu(x)=\displaystyle e^{\int h(x)\,\mathrm{d}\, x}.$
\item Si $\displaystyle \frac{\displaystyle\frac{\partial }{\partial x} N(x,y)-\displaystyle\frac{\partial}{\partial y}M(x,y)}{M(x,y)}=h(y)$
entonces $\mu(x,y)=\mu(y)=\displaystyle e^{\int h(y)\,\mathrm{d}\, y}.$
\item Si existen números $m$ y $n$ de manera que se cumple
$\displaystyle \frac{\partial M(x,y)}{\partial y}-\frac{\partial N(x,y)}{\partial x}=m\frac{N(x,y)}{x}-n\frac{M(x,y)}{y}$,
entonces $\mu(x,y)=x^my^n$.
\item Si existen funciones $P(x)$ y $Q(y)$ que satisfacen
$\displaystyle \frac{\partial M(x,y)}{\partial y}-\frac{\partial N(x,y)}{\partial x}=P(x){N(x,y)}-Q(y)M(x,y)$,
se propone $\mu(x,y)=\displaystyle e^{\int P(x)\,\mathrm{d}\, x}\displaystyle e^{\int Q(y)\,\mathrm{d}\,y}$.
\end{itemize}
\item Una vez hallado el factor integrante $\mu(x,y)$ se resuelve la ecuación exacta
$$
y^\prime=-\frac{\mu(x,y)M(x,y)}{\mu(x,y)N(x,y)}
$$
usando el método de la subsección (\ref{eq:solexacta}).
\end{enumerate}
%\fbox{\href{https://youtu.be/68WYLC5EZoA}{Video}}\\
%\fbox{\href{}{Ejemplo resuelto 1}}\\
%\fbox{\href{}{Ejemplo resuelto 2}}\\
%\fbox{\href{}{Ejemplo resuelto 3}}\\
%\fbox{\href{}{Ejemplo resuelto 4}}\\
%\fbox{\href{}{Ejemplo resuelto 5}}
\subsection{EDO de primer orden de \emph{tipo lineal}}\label{sec:lin}\label{eq:lineal}
Si en la EDO \ref{eq:normal}, la función $H(x,y)=p(x)y+q(x)$, donde $p,q$ son funciones, se tiene una EDO \emph{de tipo lineal}. Es decir,
$$
y^\prime=p(x)\,y+q(x)
$$
\begin{itemize}
\item Si $q(x)\equiv0$, la EDO anterior se reduce a
$$
y^\prime=p(x)y
$$
que es una EDO \emph{separable} (véase \ref{eq:solseparable}) y se le llama \emph{EDO de tipo lineal homogénea}.
\item Si $q(x)\not\equiv0$, se dice \emph{EDO de tipo lineal no homogénea}.
\end{itemize}
Dada la EDO
$$
y^\prime=p(x)\,y+q(x),
$$
tiene una EDO homogénea asociada
$$
y_h^\prime=p(x)y_h.
$$
Por una solución particular $y_p(x)$ a una función $y_p(x)$ que satisface la EDO
$$
y^\prime=p(x)\,y+q(x).
$$
En general, la estructura de una solución general de la EDO de tipo lineal está dada
en términos de la solución de la EDO lineal homogénea asociada y una solución particular.
Es decir, la \emph{solución general de la EDO lineal }
$$
y^\prime=p(x)\,y+q(x),
$$
es
$$
y(x)=y_h(x)+y_p(x)
$$
\subsubsection{Método (de variación de parámetros) para resolver EDO de primer orden \emph{de tipo lineal}}
\begin{enumerate}
\item Se resuelve la \emph{ecuación diferencial homogénea asociada a la EDO de tipo lineal}:
$$
\frac{\,\mathrm{d} Y}{\,\mathrm{d}x}=p(x)Y
$$
por el método para EDOS separables (véase \ref{eq:separable}) y se obtiene la solución general
$$Y(x)=ce^{\phi(x)},$$
donde $ \phi^\prime(x)=p(x)$.
\item Para la EDO de tipo lineal no homogénea
$$
y^\prime=p(x)\,y+q(x),
$$
se buscan soluciones de la forma
$$y(x)=c(x)e^{\phi(x)}.$$
\item Sustituimos las expresiones para $y$ y $y^\prime$ en la ecuación y obtenemos una EDO para la función $c(x)$
$$c^\prime(x)=q(x)e^{-\phi(x)}.$$
\item Integrando, obtenemos la familia de funciones
$$c(x)=\int\left(q(x)e^{-\phi(x)}\right)\,\mathrm{d}f x.$$
\item Sustituimos esta $c(x)$ en $y(x)$ y obtenemos la solución general de la EDO de tipo lineal:
$$
y(x)=(Q(x)+k)e^{\phi(x)}
$$
donde $\phi$ es tal que $\phi'=p$, $Q'=qe^{-\phi}$ y $k$ es una constante arbitraria.
\end{enumerate}
\fbox{\href{https://youtu.be/eeI1-aR_b0A}{Video}}\\
\fbox{\href{https://youtu.be/UW0V3nsyI4Y}{Ejemplo resuelto 1}}\\
\fbox{\href{https://youtu.be/bTlCnVcJyrc}{Ejemplo resuelto 2}}\\
\fbox{\href{https://youtu.be/cBmG2sYWsGI}{Ejemplo resuelto 3}}\\
\fbox{\href{https://youtu.be/uRniejnLiz0}{Ejemplo resuelto 4}}\\
\fbox{\href{https://youtu.be/dkNwCNGnkjk}{Ejemplo resuelto 5}}
\subsubsection{Método (de factor integrante) para resolver EDO de primer orden \emph{de tipo lineal}}
\begin{enumerate}
\item Buscamos una primitiva $P(x)$ para $-p(x)$. Es decir, $P^\prime(x)=-p(x)$.
\item Observemos que
$$
(e^{P(x)}y)^\prime=e^{P(x)}y^\prime+e^{P(x)}P^\prime(x)y=e^{P(x)}(y^\prime-p(x)y)=e^{P(x)}q(x).
$$
\item Calculamos una primitiva $R(x)$ para la función $e^{P(x)}q(x)$ de donde se tiene que
$$
(e^{P(x)}y)^\prime=R^\prime(x),
$$
de donde
$$
e^{P(x)}y=R(x)+C
$$
donde $C\in\mathbb R$
\item Se escribe la solución general de la EDO de tipo lineal:
$$
y(x)=(R(x)+C)e^{-P(x)}
$$
donde $P(x)$ es tal que $P^\prime=-p$, $R^\prime=qe^{P}$ y $C$ es una constante arbitraria.
\end{enumerate}
\subsubsection{Método para resolver EDO de primer orden \emph{de tipo lineal} usando función de Green}
\begin{enumerate}
\item Consideramos la solución de la EDO lineal homogénea asociada a la EDO de tipo lineal dada, $\displaystyle y_h(x)=e^{\int p(x)\,\mathrm{d}f x}$
\item Definimos la \emph{función de Green de orden 1}, denotada por $G_1(x,t)$ y definida por la identidad
$$
G_1(x,t)=\frac{y_h(x)}{y_h(t)}.
$$
\item Calculamos la \emph{solución particular} $y_p$ dada por
$$
y_p(x)=\int G_1(x,t)f(t)\,\mathrm{d} t.
$$
\item Escribimos la solución general de la EDO de tipo lineal como $y(x)=y_h(x)+y_p(x)$
\end{enumerate}
El método por función de Green es equivalente al método por variación de parámetros.
\subsection{EDO de primer orden \emph{de tipo Bernoulli}}
Si en la EDO \ref{eq:normal}, la función $H(x,y)=p(x)y+q(x)y^n$, donde $p,q$ son funciones y $\alpha\in\mathbb R$, se tiene una EDO de primer orden \emph{de tipo Bernoulli}. Es decir,
$$
y^\prime=p(x)y+q(x)y^n.
$$
Si en la EDO, $n=0$ o $n=1$; la ecuación se reduce a una EDO de tipo lineal \ref{eq:lineal} (no homogénea en el caso $\alpha=0$ y homogénea en el caso $n=1$).
A continuación mostraremos el método para resolver las ecuaciones de tipo Bernoulli cuando $n\not=0,1$.
\subsubsection{Método para resolver EDO de primer orden \emph{de tipo Bernoulli}}
Supongamos que en la EDO de primer orden \emph{de tipo Bernoulli}
$$
y^\prime=p(x)y+q(x)y^n.
$$
se tiene que $n\not=0,1$.
\begin{enumerate}
\item Consideramos el cambio de variable $u=y^{1-n}$ y por tanto
$$y^\prime=\frac{y^n}{1-n}u^\prime.$$
\item Sustituimos lo anterior en la EDO dada y se obtiene la EDO de tipo lineal \ref{eq:lineal}
$$
u^\prime=(1-n)p(x)u+(1-n)q(x).
$$
\item Se resuelve la EDO anterior usando alguno de los métodos de la subsección \ref{sec:lin}.
\item A la solución obtenida en el paso anterior, se realiza el cambio de variable.
\end{enumerate}
\fbox{\href{https://youtu.be/5O7-MhhEAc8}{Video}}\\
\fbox{\href{https://youtu.be/I0zugJaO8tY}{Ejemplo resuelto 1}}\\
\fbox{\href{https://youtu.be/E2w02JB47ok}{Ejemplo resuelto 2}}\\
\fbox{\href{https://youtu.be/_QPZoiiKn9o}{Ejemplo resuelto 3}}\\
\end{document}