


En general una función es una regla o forma de asociar elementos de un conjunto con elementos de otro conjunto, de tal manera que a un elemento del primer conjunto le corresponda sólo un elemento del segundo conjunto.
Cuando los dos conjuntos son de números reales se tiene una función real de variable real que suele denotarse como $y = f ( x )$, donde $x$ está en el primer conjunto y se le llama variable independiente y $y$ está en el segundo conjunto y se le llama variable dependiente o función.
Por ejemplo la función: todo número asociado con su doble, así el $1.3$ quedará asociado con el $2.6$; el $–1$ con el $–2$; etc.
Se denotará la función como $y = f ( x ) = 2 x$
y se tiene que $y = f ( 1.3 ) = 2(1.3)=2.6$;
$y= f ( -1 ) = 2(-1)=- 2$; etc.
El dominio de una función (real de variable real) $y=f(x)$, es el conjunto de valores de $x$ para los que la función puede dar una imagen: $y$, es decir, $f(x)$ puede ser evaluada en un número real $x$ y producir a su vez otro número real $y=f(x)$.
 |
 |
 |
|---|---|---|
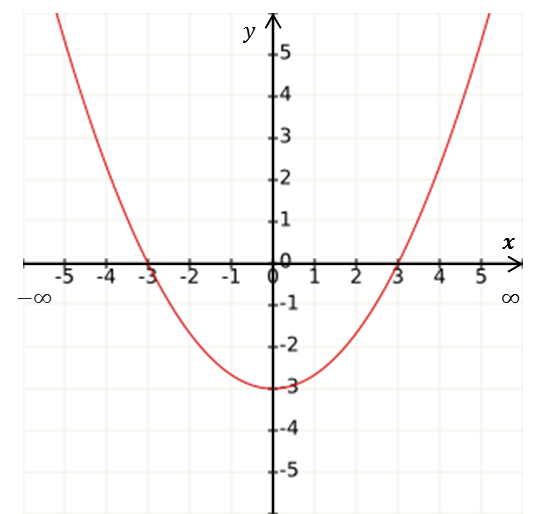
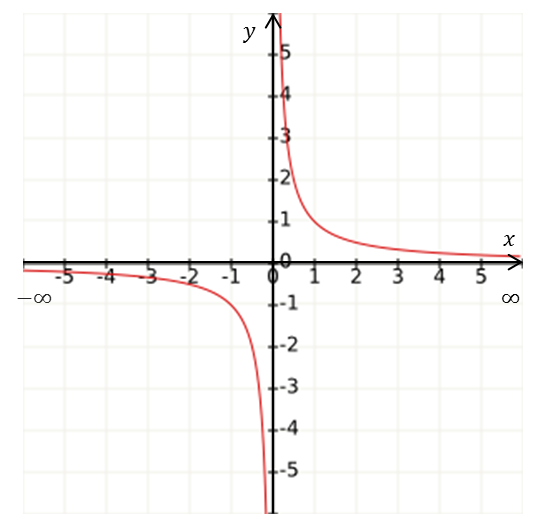
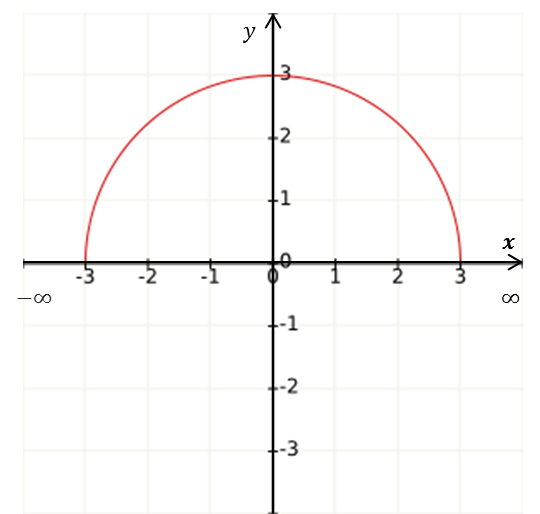
| $D_f=(-\infty,\infty)$ | $D_f=(-\infty,0)\cup(0,\infty)$ | $D_f=[-3,3]$ |
Gráficamente son los valores de $x$ que tienen una $y$ asociada, esto es, los intervalos del eje $x$ donde hay gráfica.
Para obtener el dominio de una función recordamos que de manera general, en expresiones del tipo:
Las raíces o ceros de una función son los valores en el dominio cuya imagen es cero, esto es, valores de $x=r_{i}$ que hacen $f(r_{i})=0$ con $r_{i}\in D_{f}$ .
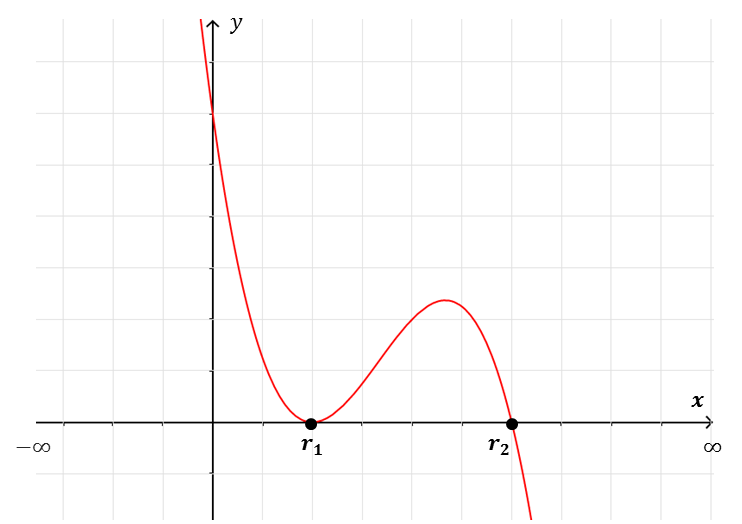
Gráficamente las raíces reales se identifican como la abscisa (valor de $x$) de los puntos donde la gráfica toca o corta al eje $x$.
La multiplicidad de una raíz, es decir, el número de veces que cuenta como raíz de una función polinomial, es igual al número de factores lineales iguales en la factorización del polinomio, correspondientes a esa raíz.
Un polinomio de grado n tiene n raíces reales y/o complejas, y puede factorizarse en términos de ellas.
Factorización: La factorización de un polinomio en $x$ de grado $n$, $P_n(x)=a_{n}x^n+a_{n-1}x^{n-1}+...+a_{1}x+a_{0}$, en términos de sus $n$ raíces (reales y/o complejas), $r_1, r_2, ... r_n$, es su expresión como el producto del coeficiente del término de grado $n:a_n$, multiplicado por los $n$ factores de la forma: $x$ menos la raíz (para cada una de las raíces reales y/o complejas), $P_n (x)=a_n(x-r_1)(x-r_2)...(x-r_n)$.
Cuando no se conocen todas las raíces o únicamente interesa factorizar en términos de las raíces reales, se puede hacer una factorización parcial como $P_n (x)=(x-r_1)Q_{n-1} (x)$...(1).
Donde $Q_{n-1}(x)$ es otro polinomio de grado $n-1$ , que se obtiene al dividir $P_n (x)$ entre $x-r_1$ , como puede verse de (1). Este proceso puede repetirse buscando ahora las raíces de $Q_{n-1}$ y continuar hasta donde sea posible.
La paridad de una función puede verse como una especificación de simetría de su gráfica, la definición es la siguiente.
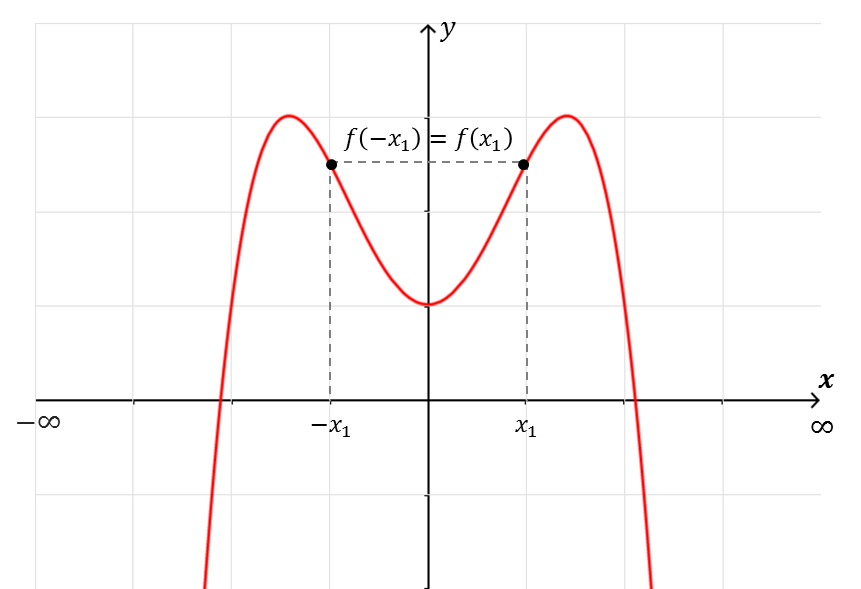 |
|---|
Su gráfica tiene simetría con respecto al eje $y$ (si se doblara la gráfica en el eje $y$, las dos partes coincidirían).
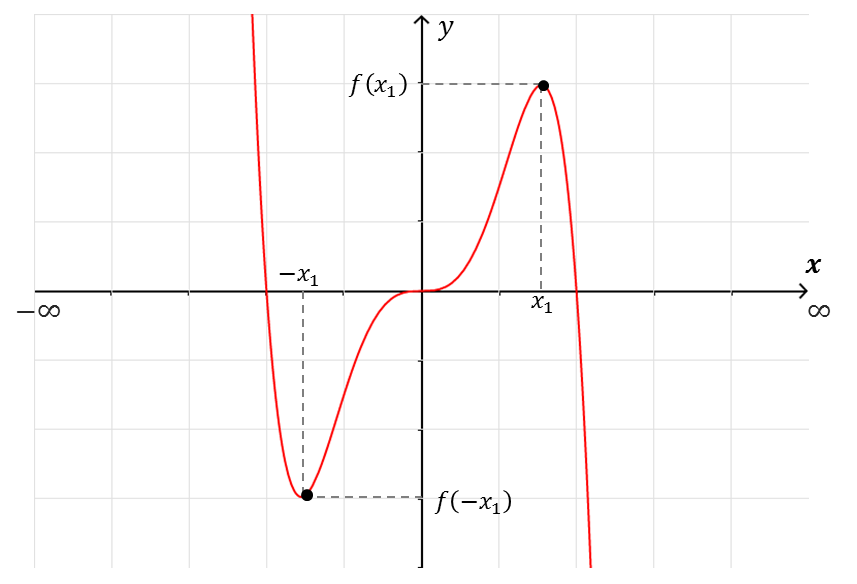 |
|---|
| $f(-x_1)=-f(x_1)$ |
Su gráfica tiene simetría con respecto al origen (cualquier recta que pase por el origen, corta a la gráfica de la misma forma de un lado del origen, que del otro, esto es, a la misma distancia y en el mismo número de puntos).
Encontrar la paridad de una función es importante, puesto que si la función por analizar resulta ser par o impar, bastará con analizarla para valores positivos y cero de $x$ y por el tipo de simetría se puede concluir para los valores negativos.
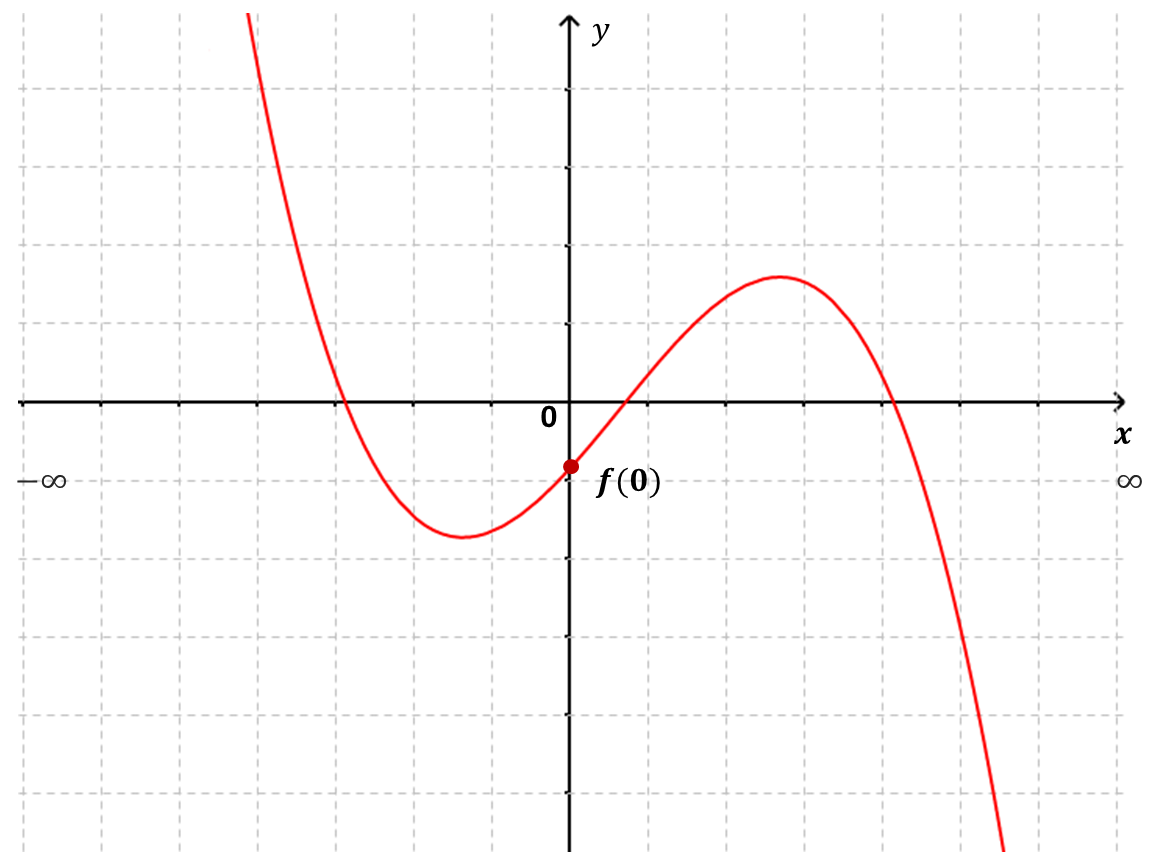
Punto de corte al eje $y$: El punto donde la gráfica de la función $y=f(x)$ corta al eje $y$ es la evaluación de la función en $x=0$, esto es $y=f(0)$.
Asíntotas horizontales
Si el límite de la función cuando $x$ tiende a infinito o menos infinito es igual a una constante, entonces la función tiene una asíntota horizontal de ecuación: $y$ igual a la constante, esto es:
Si $\underset{x\to-\infty}{\lim} f(x)=k$ entonces $y=k$ es una asíntota horizontal de $f(x)$.
Si $\underset{x\to\infty}{\lim} \;f(x)=p$ entonces $y=p$ es una asíntota horizontal de $f(x)$.
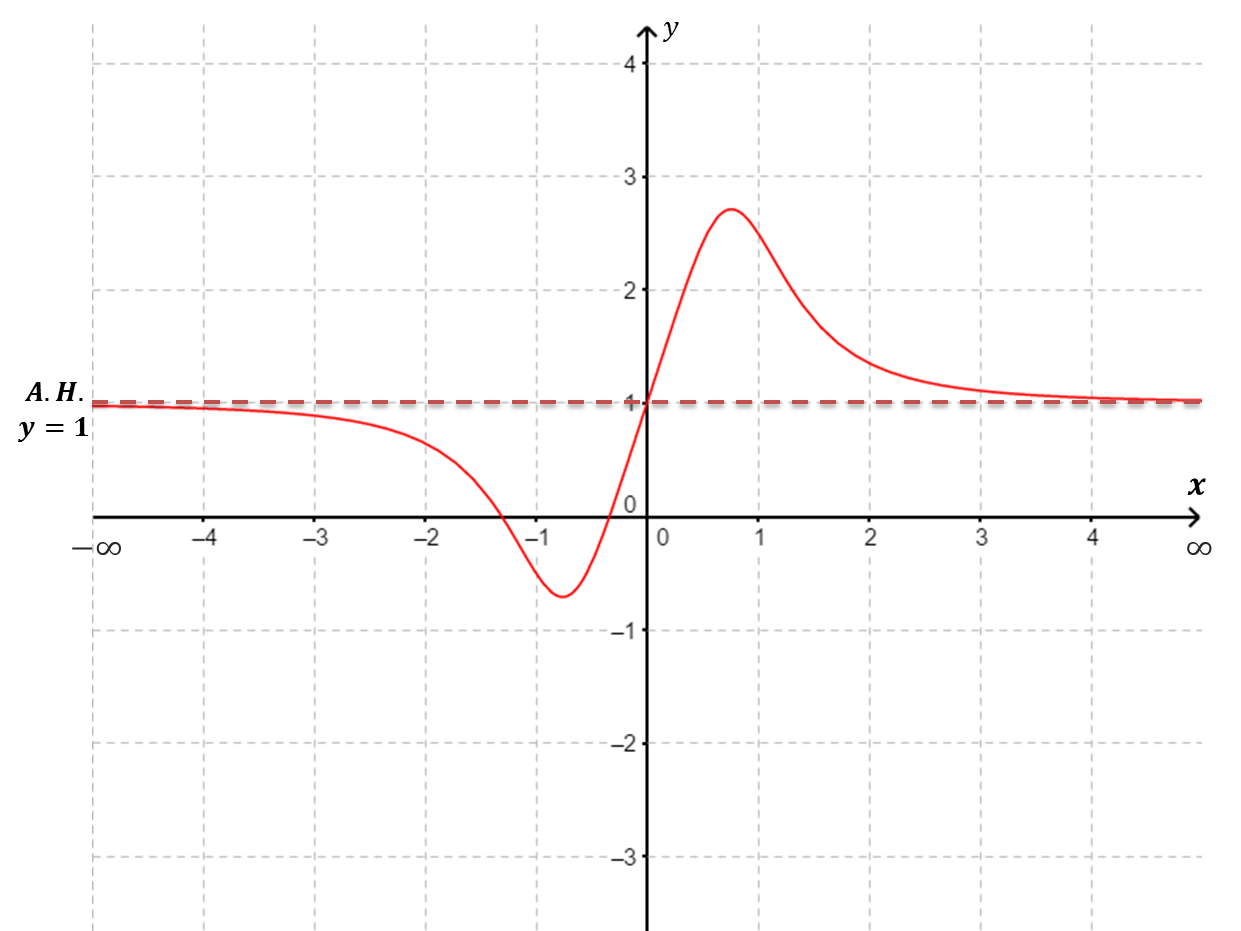 |
 |
|---|---|
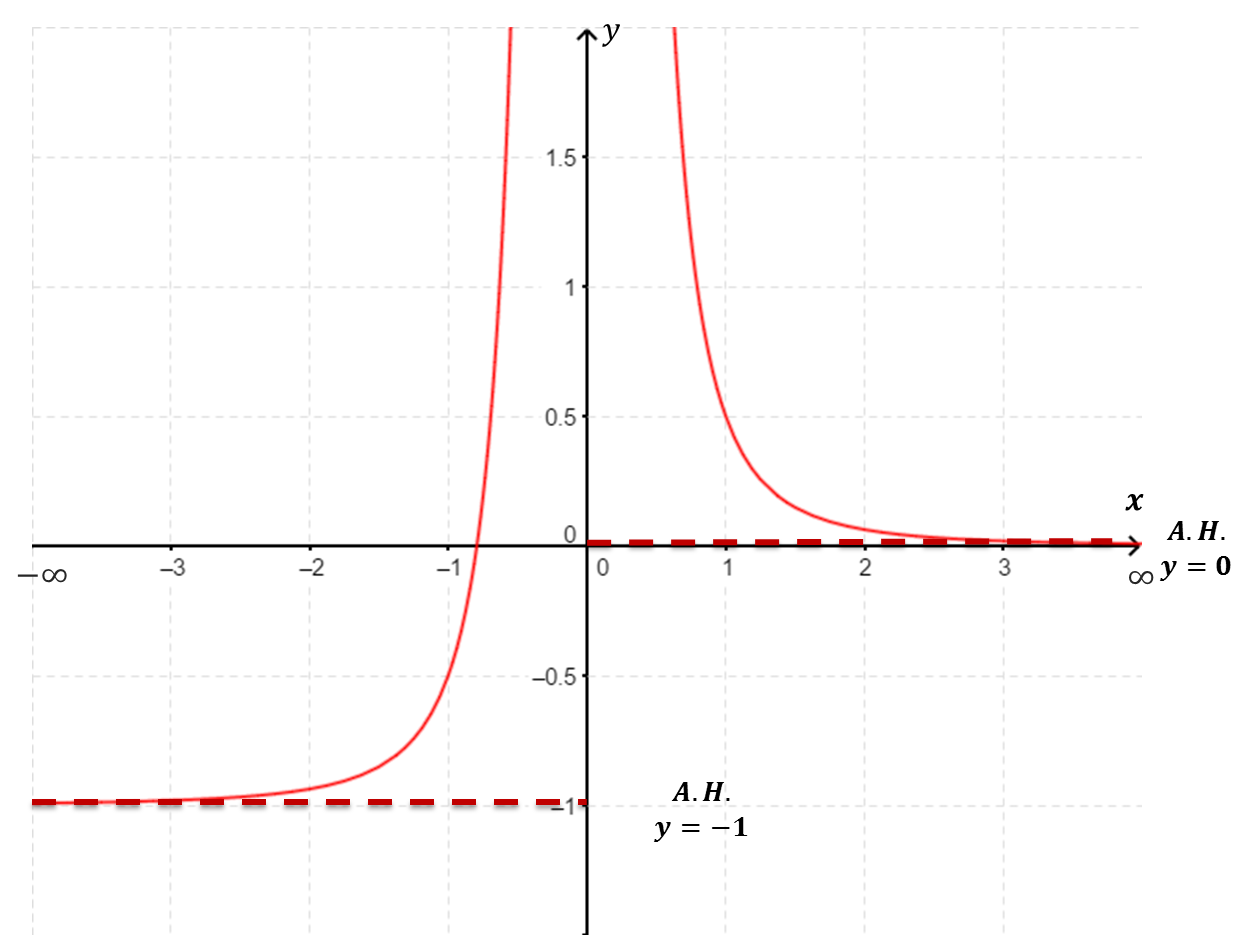
| $f(x)$ tiene una asíntota horizontal de ecuación y=1 $\underset{x\to \infty}{\lim} f(x)=1$ y $\underset{x\to -\infty}{\lim} f(x)=1$. |
$f(x)$ tiene una asíntota horizontal de ecuación $y=-1$ y $y=0$ $\underset{x\to \infty}{\lim} f(x)=0$ y $\underset{x\to -\infty}{\lim} f(x)=-1$. |
Asíntota Verticales
Si el límite de la función cuando $x$ tiende a una constante (valores de $x$ que genere una división entre cero en la función) es igual a infinito positivo o negativo (aunque sea en forma lateral), entonces la función tiene una asíntota vertical de ecuación $x$ igual a la constante, esto es:
Si $\underset{x\to m}{\lim} \;f(x)=\infty$, $\underset{x\to m}{\lim} \;f(x)=-\infty$, o $\underset{x\to m}{\lim} \;f(x)=\not\exists $, con límites laterales infinitos.
Entonces $x=m$ es una asíntota vertical de $f(x)$.
($m$ es un valor de $x$ que genera una división entre cero en la función)
 |
 |
|---|---|
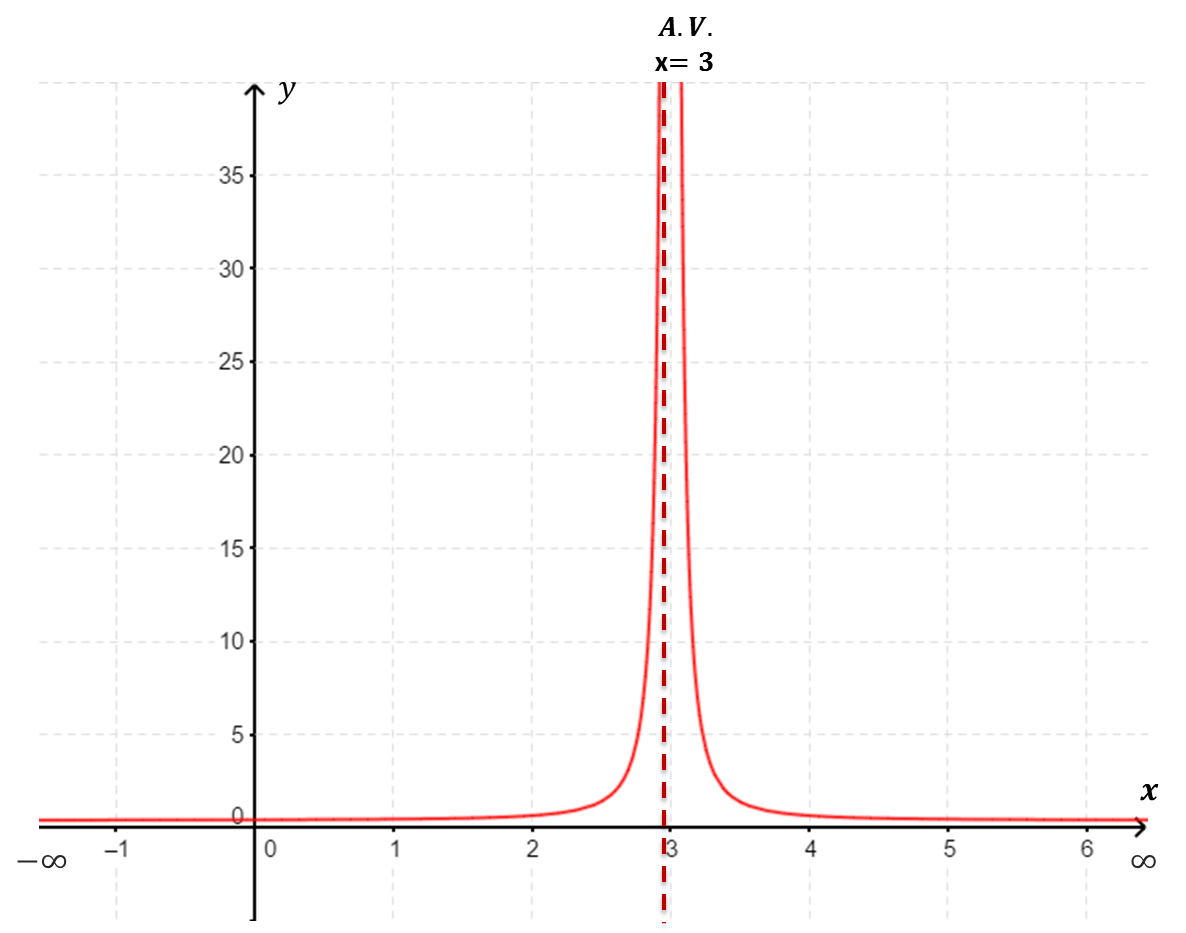
| $f(x)$ tiene una asíntota vertical de ecuación $x=3$ ( $\underset{x\to 3}{\lim} \;f(x)=\infty$). | $f(x)$ tiene una asíntota vertical de ecuación $x=2$ ( $\underset{x\to 2^{+}}{\lim} f(x)=-\infty$ y $\underset{x\to 2^{-}}{\lim} f(x)=\infty$) |
El Esbozo gráfico de una función es la representación gráfica aproximada de la función en un sistema de ejes coordenados, es decir, el conjunto de todos los puntos coordenados $(x,y)$ definidos por la función $y=f(x)$.
Un buen esbozo gráfico debe mostrar los puntos donde la gráfica tiene algún cambio de comportamiento, ajustando la escala de forma conveniente.
De manera general, para hacer el esbozo gráfico se toma en cuenta la información que se pueda obtener analíticamente y se complementa obteniendo algunos de sus puntos coordenados evaluando la función, es decir, dar algunos valores para $x$ y calcular los valores correspondientes de $y$, lo que se llama comúnmente tabular la función.
Conforme se conozcan más elementos de la función, obtenidos analíticamente, se necesitarán menos tabulaciones para tener un buen esbozo gráfico.
El rango (o contradominio) de la función $y =f(x)$ es el conjunto de todas las imágenes, esto es, el conjunto de todos los valores de la variable $y$ que están asociadas a algún valor de $x.$
 |
 |
|---|---|
| El rango es el conjunto de las $y\in[-3,\infty)$ | El rango es el conjunto de las $y\in[0,3]$ |
Gráficamente el rango son los valores de $y$ asociados a los valores de $x$, esto es, los intervalos en el eje $y$ donde hay gráfica.
La monotonía de una función se refiere a su crecimiento o decrecimiento.
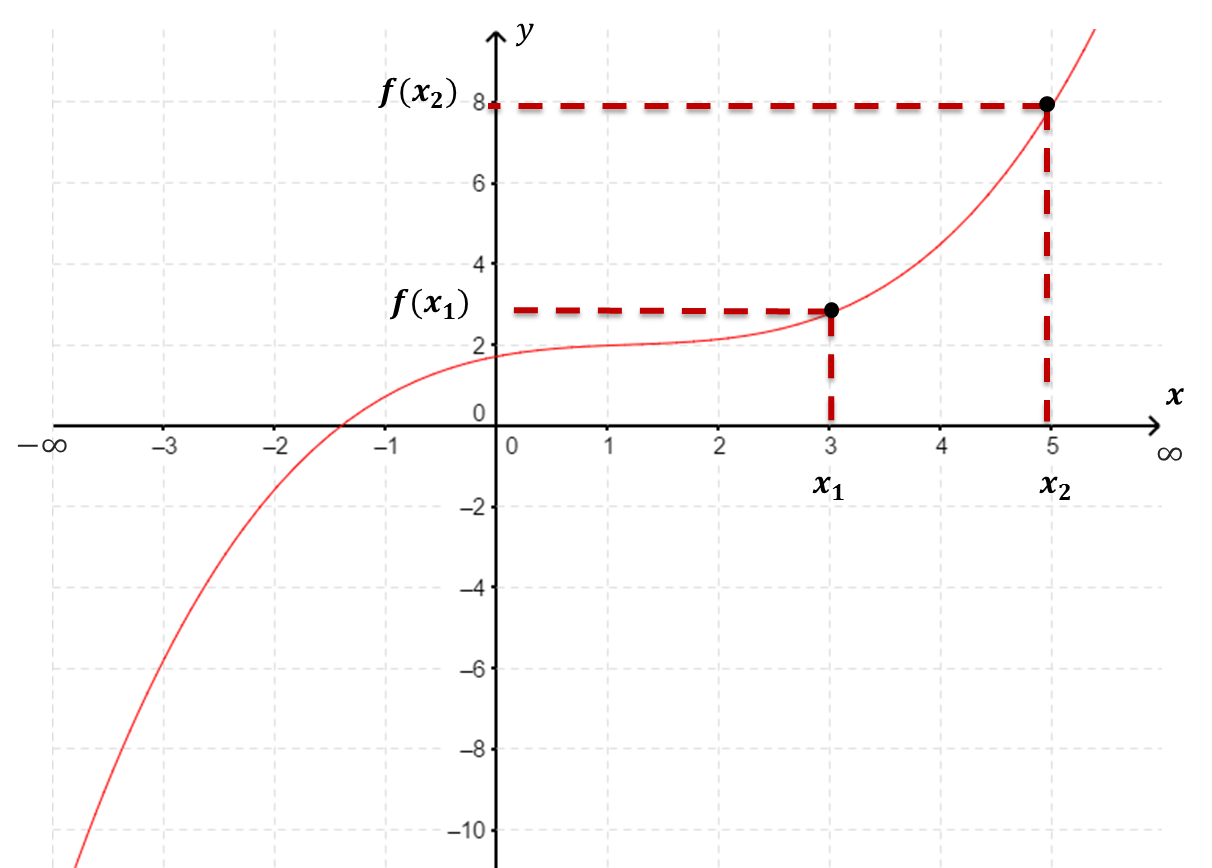
Se dice que $\boldsymbol{f(x)}$ es creciente en un intervalo $J$
si para toda $ x_2 > x_1 \in J$ se cumple que $f(x_2) > f(x_1)$.
 |
|---|
| Función Creciente. |
Gráficamente, la curva sube en el intervalo $J$ (vista de izquierda a derecha, como lo indica el sentido positivo del eje $x$).
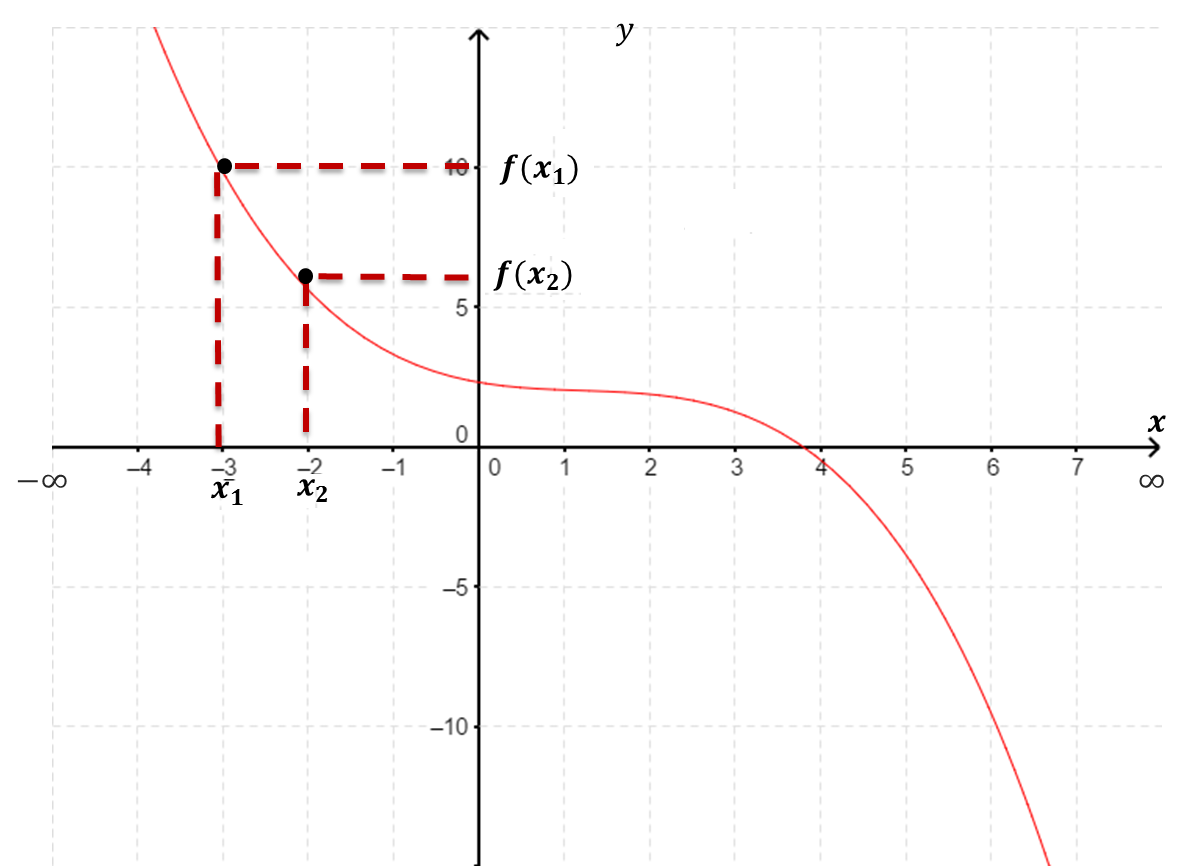
Se dice que $\boldsymbol{f(x)}$ es decreciente en un intervalo $J$
si para toda $ x_2 > x_1 \in J$ se cumple que $f(x_2) < f(x_1)$.
 |
|---|
| Función Decreciente. |
Gráficamente, la curva baja en el intervalo $J$ (vista de izquierda a derecha, como lo indica el sentido positivo del eje $x$).
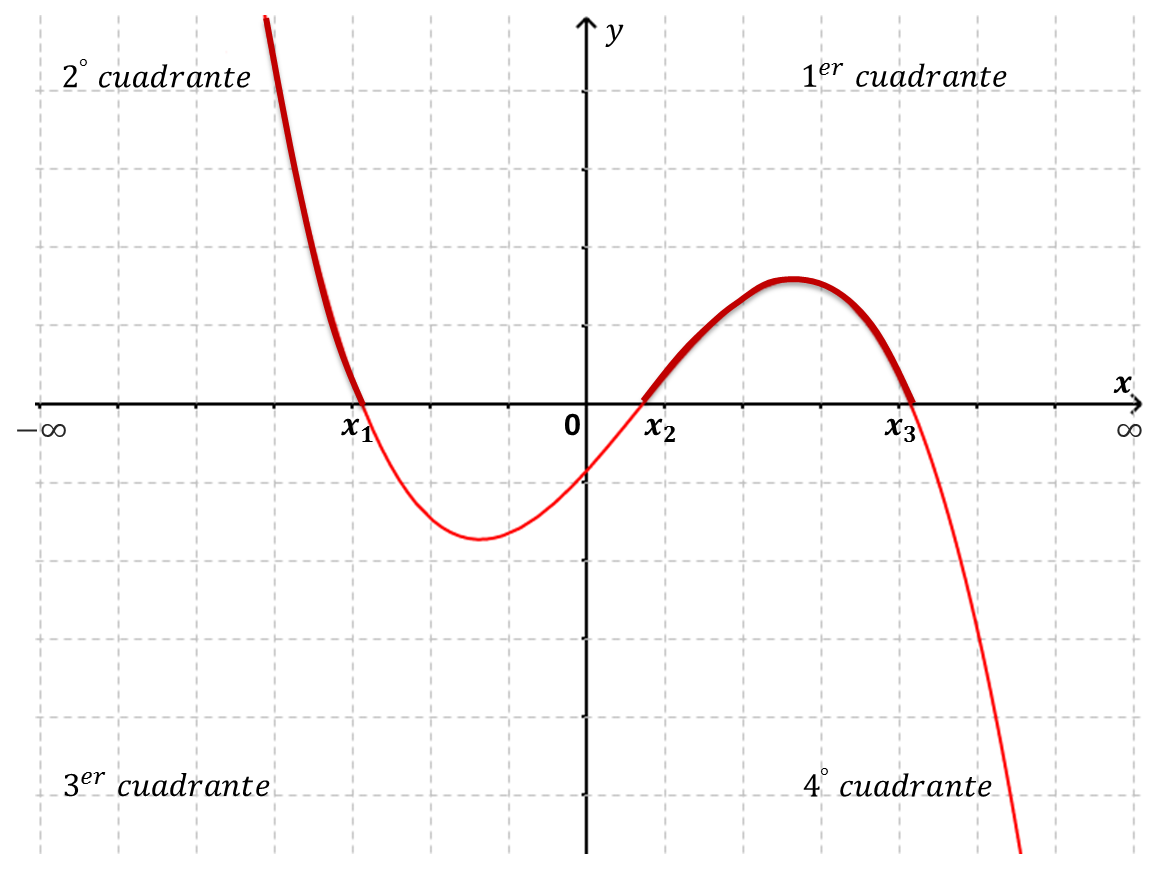
Intervalos donde la función es positiva o negativa: Los intervalos donde la función toma valores mayores que cero $\boldsymbol{f(x)>0}$ son los intervalos definidos por los valores de $x$ para los cuales sus imágenes, las $y$ correspondientes, son mayores que cero. Esto es, la resolución de la desigualdad $y=f(x)>0$.
 |
|---|
| $y=f(x)>0$ para $x\in(-\infty ,x_1) \cup (x_2,x_3) $ |
Geométricamente, como los puntos sobre el eje $x$ tienen $y=0$, la porción de la gráfica de $f(x)$, correspondiente a los valores positivos de la función, se encontrará por arriba del eje $x$ (en el 1º y/o 2º cuadrantes del sistema de ejes coordenados) donde la ordenada (valor de $y$ ) de todos los puntos coordenados, es positiva.
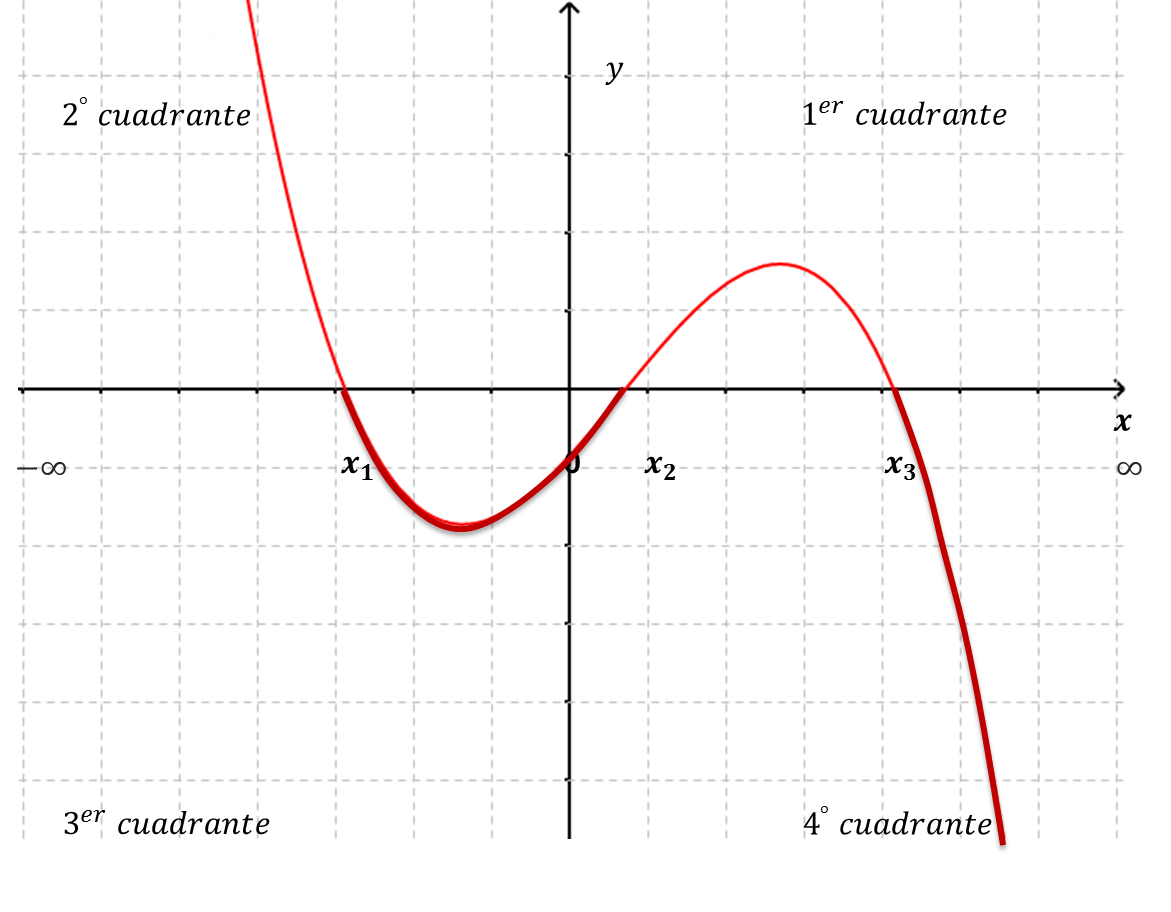
Los intervalos donde la función toma valores menores que cero $\boldsymbol{f(x)<0}$ son los intervalos definidos por los valores de $x$ para los cuales sus imágenes, las $y$ correspondientes, son menores que cero. Esto es, la resolución de la desigualdad $y=f(x)<0$ .
 |
|---|
| $y=f(x)<0$ para $x\in(x_1,x_2) \cup (x_3,\infty) $ |
Geométricamente, como los puntos sobre el eje $x$ tienen $y=0$ la porción de la gráfica de $f(x)$, correspondiente a los valores negativos de la función, se encontrará por abajo del eje $x$ (en el 3º y/o 4º cuadrantes del sistema de ejes coordenados) donde la ordenada (valor de $y$) de todos los puntos coordenados, es negativa.