Función polinomial

Un polinomio es una función que tiene la forma: $$f(x)=a_n x^n + a_{n-1} x^{n-1}+...+a_2 x^{2}+a_1 x+ a_0$$

donde $a_i$ son constantes reales y $n$ es un entero positivo.

De manera general ya se puede decir que:

Tienen dominio $D_f=(\;-\infty,\;\infty)$, a menos que se indique explícitamente otro.

Son funciones continuas en todo su dominio porque: $$\lim_{x\rightarrow c}\;a_nx^n+a_{n-1}x^{n-1}+...+a_2x^2+a_1x+a_0=$$ $$a_nc^n+a_{n-1}c^{n-1}+...+a_2c^2+a_1c+a_0\;=f(c)$$ para $c∈D_f$

No tienen asíntotas verticales ya que ningún valor de $x$ genera una división entre cero.

No tienen asíntotas horinzontales, los límitas de un polinomio cuando $x$ tiende a infinito o a menos infinito son también infinitos (positivos y/o negativos).

Las funciones constantes $f(x)=a_0$ tienen como grafica una recta horizontal que corta al eje $y$ en $a_0$.

Los polinomios de primer grado: $f(x)=a_1x+a_0$ tienen como gráfica una recta con pendiente $a_1$ y corte al eje $y$ en $a_0$.

Los polinomios de segundo grado:$f(x)=a_2x^2+a_1x+a_0$ tiene como gráfica una párabola (con eje de simetría vertical) que:

tienen ceros o raíces (puntos de corte al eje $x$) en $x_{1,2}=\frac{-a_1±\sqrt{{a_2}^2-4a_1a_0}}{2a_1}$ o no, si ${a_2}^2-4a_1a_0 <0$,

corte al eje $y$ en $a_0$

tiene vértice en $(x_v, y_v)$ donde $x_v=\frac{-a_1}{2a_2} $ y $y_v=f(x_v)$;

abre hacia arriba si $a_2>0$ y abre hacia abajo si $a_2<0$ (ver desigualdades de segundo grado)

Ejemplo:

Para la función $f(x)=2x^3-8x$ (polinomio de tercer grado con $a_3=2$, $a_2=0$, $a_1=-8$, y $a_0=0$.

Obtener el dominio, los ceros o raíces, la paridad, el punto de corte al eje $y$, las asíntotas verticales y horizontales, los intervalos de continuidad y clasificación de discontinuidades, el esbozo gráfico, el rango, la monotonía y los intervalos donde es positiva o cero y donde es negativa.

Dominio: el dominio de la función son todos los reales, $x\in\mathbb{R}$ o $D_f=(-\infty,\infty)$, ya que para todo valor de $x$ en los reales se puede obtener su valor correspondiente de $y$ .

Ceros o raíces: $y=f(x)=0$;

                        $2x^3-8x=0$
                        $2x(x^2-4)=0$
                        $x=0$    $x^2=4$
                                      $x=\pm2$

Las raices de la fución son: $x=-2$, $x=0$ y $x=2$.

Paridad: $f(-x)=2(-x)^3-8(-x)$
                         $=-2x^3+8x$
                         $=-(2x^3-8x)$
                         $=-f(x)$
$f(x)$ es impar, su gráfica es simétrica con respecto al origen.

Punto de corte al eje $\boldsymbol{y}$:
$y=f(0)=2(0)^3-8(0)=0$ el punto tiene coordenadas (0,0) que es el origen.

Asíntotas verticales: no tiene, ya que ningún valor de $x$ genera una división entre cero en la función.

Asíntotas horizontales: $$\lim_{x\rightarrow \infty} 2x^3-8x: \;\infty -\infty: indeterminado$$ $$\lim_{x\rightarrow \infty} x^3(2-\frac{8}{x^2})=\infty(2-0)=\infty\;\;\;\;\;\;\;\;\;\;$$ $$\lim_{x\rightarrow -\infty} x^3(2-\frac{8}{x^2})=-\infty(2-0)=-\infty\;\;\;\;$$
$f(x)$ no tiene asíntotas horizontales.

Intervalos de continuidad: $f(x)$ es continua en todos los reales ya que $$\lim_{x\rightarrow a} 2x^3-8x=2a^3-8a=f(a)$$ para todo valor de $a$ en los números reales.

Clasificación de discontinuidades: la función no tiene puntos de discontinuidad.

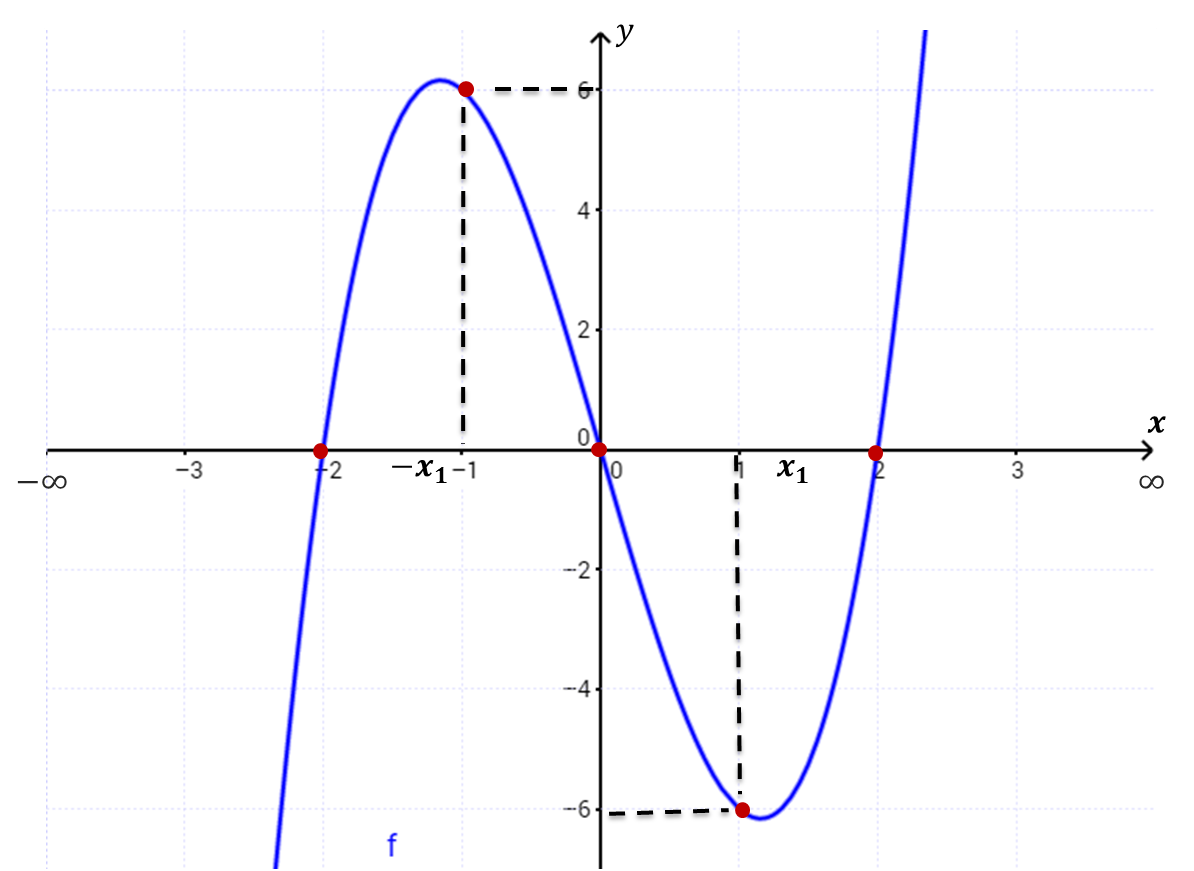
Esbozo gráfico
Tomando en cunta todos los resultados anteriores y tabulando un par de puntos:

$f(-1)=2(-1)^3-8(-1)=6$, $f(1)=2(1)^3-8(1)=-6$ .

Rango: $y=\in\mathbb{R}$ o Rango$=(-\infty,\infty)$,

Monotonía: $y=f(x)$ crece para $x\in(-\infty,-x_1]$ (los valores de $y$ aumentan, vistos de izquierda a derecha como lo indica el sentido positivo del eje $x$). Le llamamos $x_1$, al valor de $x$ donde la curva da vuelta porque todavía no los podemos calcular analíticamete.
y=f(x) decrece para $x\in[-x_1,x_1]$ (los valores de $y$ disminuyen, vistos de izquierda a derecha como lo indica el sentido positivo del eje x).

$y=f(x)$ crece para $x\in[x_1,\infty)$

Intervalos donde la función es positiva o cero y donde es negaiva.

De la gráfica se puede ver que

$\boldsymbol{y=f(x)\geq0:}$ para $x\in[-2,0]\cup[2,\infty)$