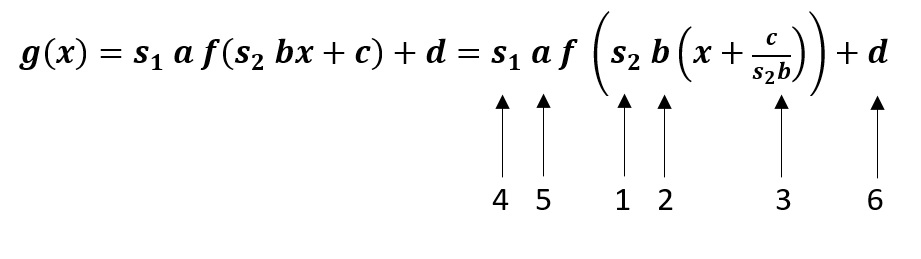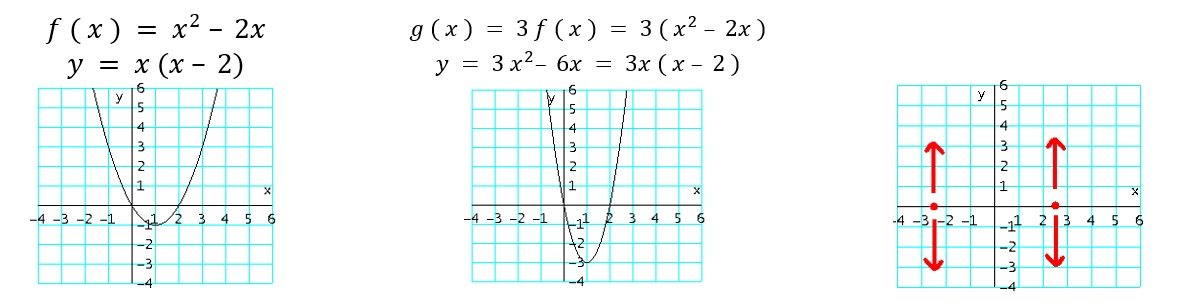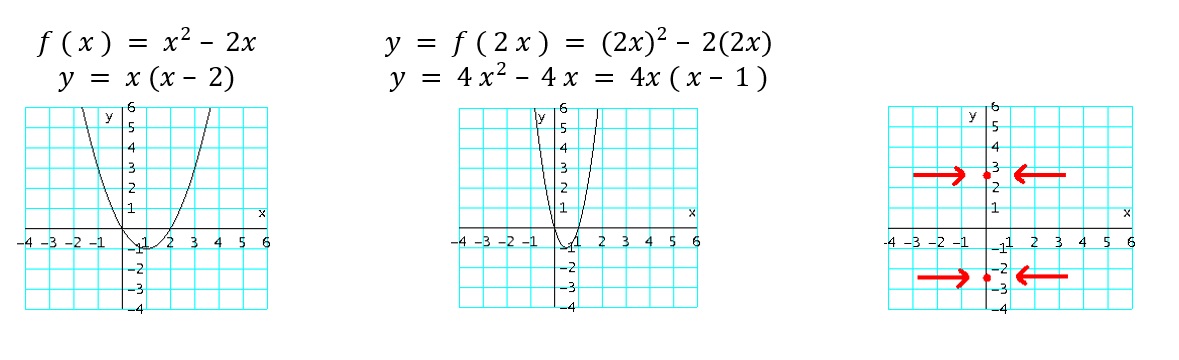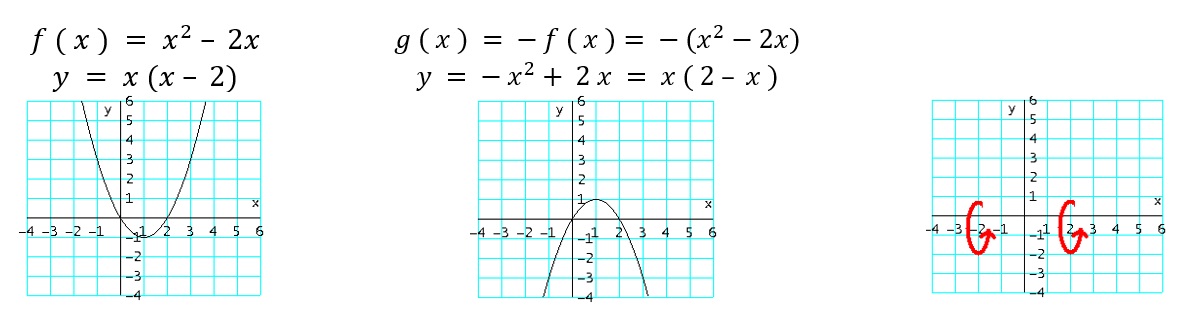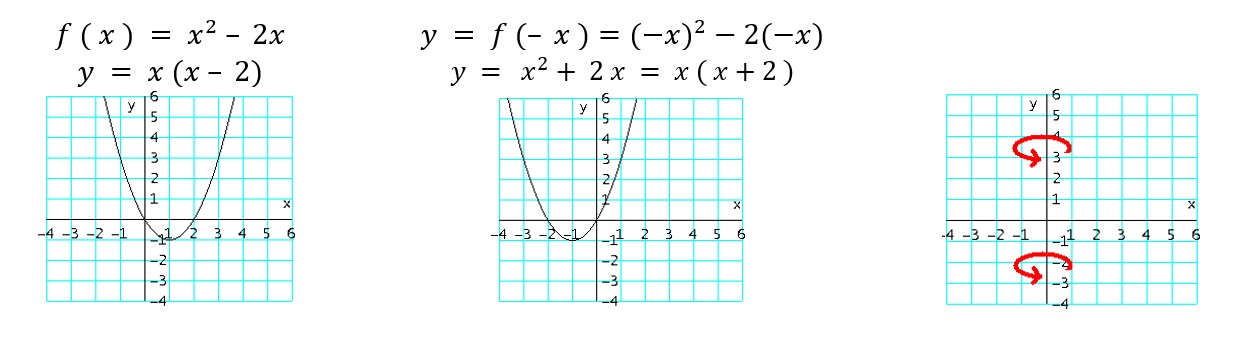Operaciones Gráficas de Funciones
Si se conoce la gráfica de la función $\boldsymbol{y=f(x)}$ y se define otra función
$\boldsymbol{g\;(x)=s_1\;a\;f(s_2\;b\;x+c)+d}$, en la que:
$\boldsymbol{s_1\;y\;s_2}$ representan un signo positivo o negativo,
$\boldsymbol{a\;y\;b}$ dos números reales positivos,
$\boldsymbol{f}$ es la función conocida con variable independiente x,
$\boldsymbol{c\;y\;d}$ dos números reales (positivos, negativos o cero).
Se puede obtener la gráfica de $\boldsymbol{g\;(x)}$ partiendo de la gráfica de $\boldsymbol{f(x)}$, aplicando sucesivamente operaciones gráficas, que se mencionan en seguida y se describen en detalle
cada una de ellas posteriormente.
El orden en que deben ejecutarse las operaciones es primero las del argumento de la función, en el que conviene factorizar el coeficiente de $x$ para proceder de izquierda a derecha
y luego hacia afuera, como se indica a continuación:
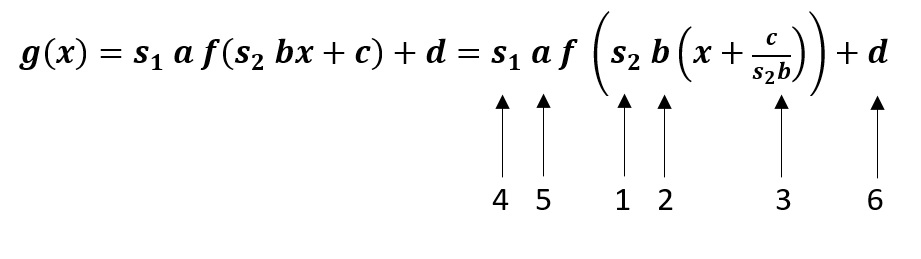
- Si $s_2$ es un signo negativo reflejar la gráfica de $f$ en el eje $y$, si es positivo no la afecta.
- Si $b > 1$ comprimir horizontalmente la gráfica anterior en un factor de $b$; si $b < 1$ alargar horizontalmente.
- Si $\frac{c}{(s_2 b)} > 0$ trasladar a la izquierda $\frac{c}{(s_2 b)}$ unidades la gráfica anterior; si es negativo trasladar a la derecha.
- Si $a > 1$ alargar verticalmente la gráfica anterior en un factor de $a$; si $a < 1$ comprimir verticalmente.
- Si $s_1$ es negativo reflejar en el eje $x$ la gráfica anterior, si es positivo no la afecta.
- Si $d$ es positivo trasladar hacia arriba $d$ unidades la gráfica anterior; si es negativo trasladar hacia abajo.
Esta traslación vertical es la última operación que debe aplicarse.
Nota. Hay otras posibilidades correctas para ejecutar el orden de las operaciones, pero cuidado, no cualquier orden es correcto.
A continuación se describen las operaciones gráficas y se da un ejemplo partiendo de una función sencilla, polinomio de segundo grado cuya gráfica es una parábola, se muestran las gráficas, se comprueba analíticamente y se describe el tipo de movimiento.
- TRASLACIONES VERTICALES para $c > 0$:
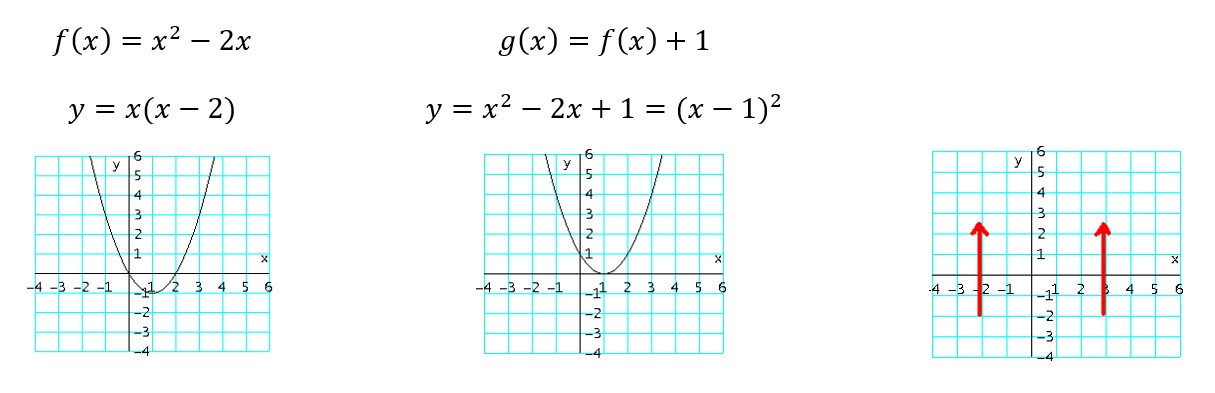
- $g_1 ( x ) = f ( x)+c$ :sube la gráfica de $f$, $c$ unidades (sumando $c$ a los valores de $y$).
Ejemplo:
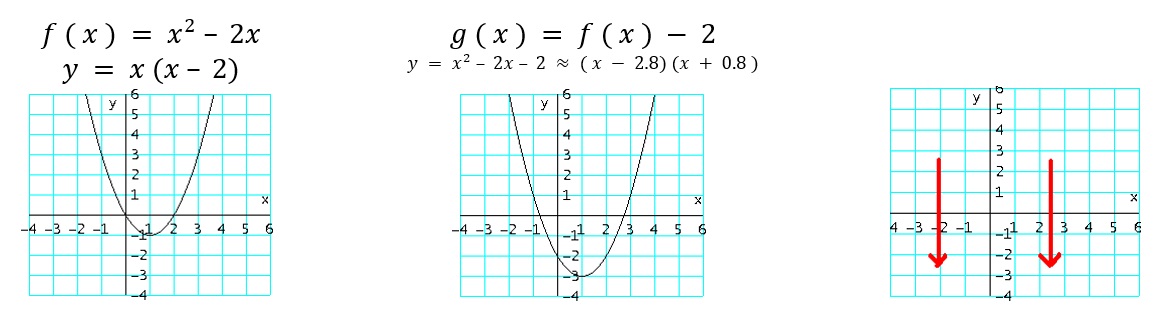
- $g_2 ( x ) = f ( x ) - c$ :baja la gráfica de $f$, $c$ unidades (restando $c$ a los valores de $y$).
Ejemplo:
- TRASLACIONES HORIZONTALES para $c > 0$:
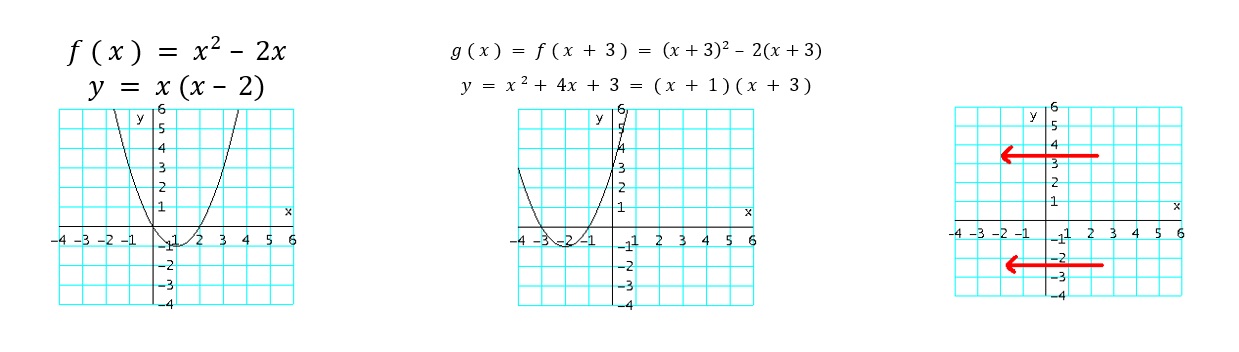
- $g_3 ( x ) = f ( x + c )$: mueve la gráfica de $f$, $c$ unidades a la izquierda (restando $c$ a los valores de $x$).
Ejemplo:
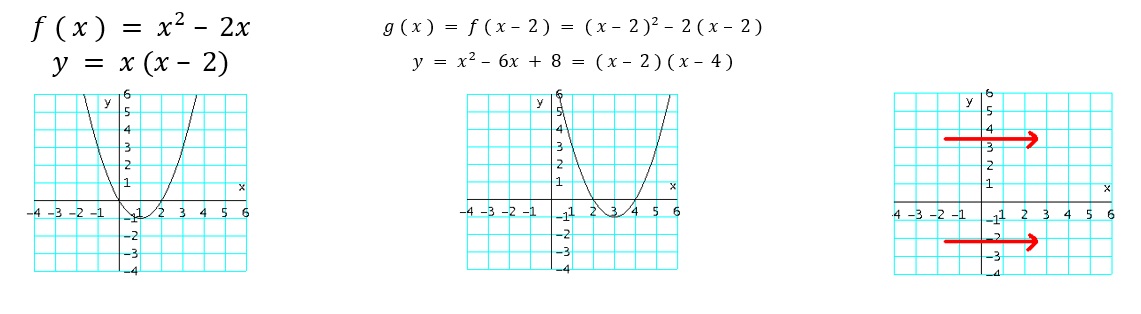
- $g_4 ( x ) = f ( x − c )$ : mueve la gráfica de $f$, $c$ unidades a la derecha (sumando $c$ a los valores de $x$).
Ejemplo:
- ALARGAMIENTOS Y COMPRESIONES VERTICALES para $c > 1$
- $g_5 ( x ) = c f ( x )$ : alarga verticalmente la gráfica de $f$, $c$ unidades (multiplicando por $c$ los valores de $y$).
Ejemplo:
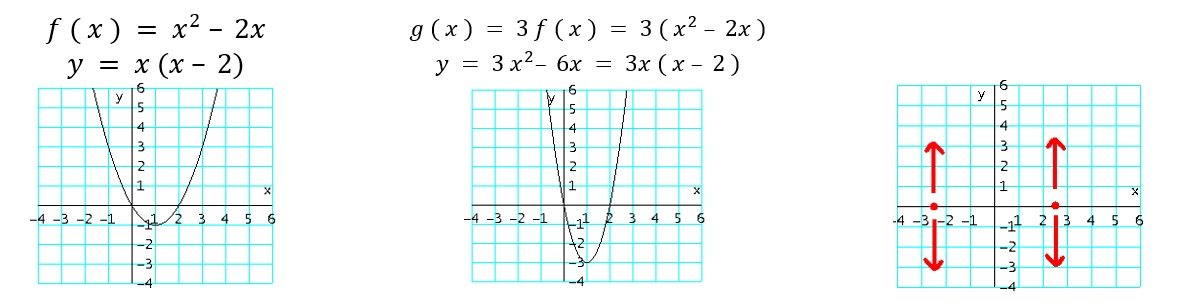
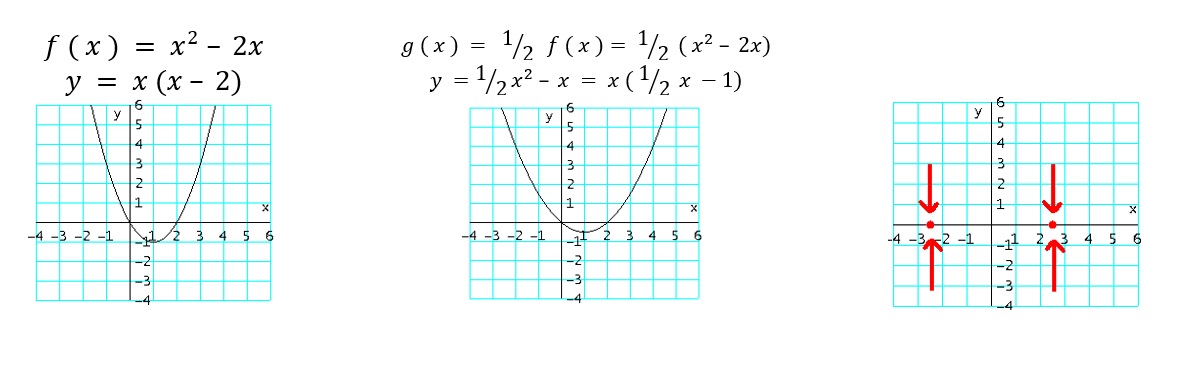
- $g_6 ( x ) =\frac{1}{C} f ( x )$ : comprime verticalmente la gráfica de $f$ , $c$ unidades (multiplicando por $\frac{1}{C}$ los valores de $y$).
Ejemplo:
- ALARGAMIENTOS Y COMPRESIONES HORIZONTALES para $c > 1$
- $g_7 ( x ) = f ( c x)$: comprime horizontalmente la gráfica de $f$, $c$ unidades (multiplicando por $\frac{1}{C}$ los valores de $x$).
Ejemplo:
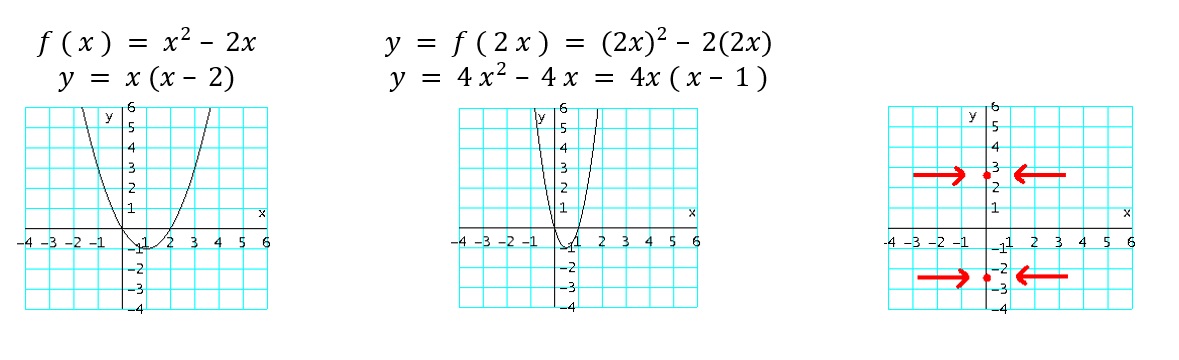
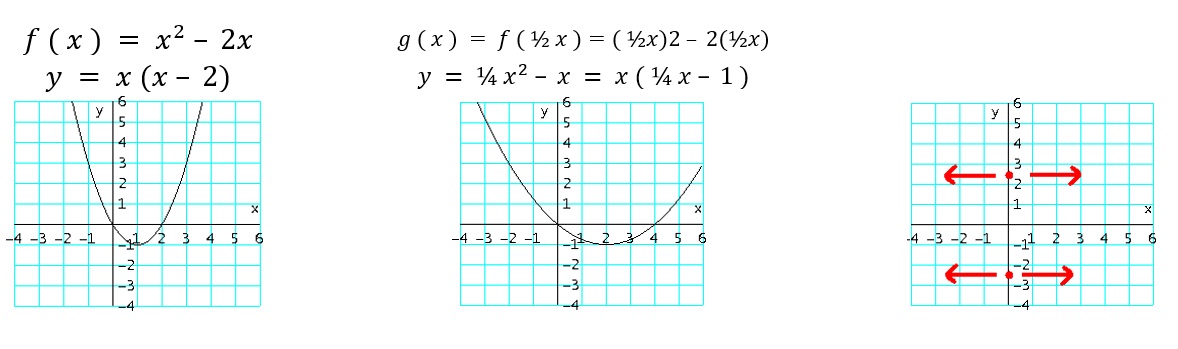
- $g_8 ( x ) = f ( \frac{1}{C} x )$: alarga horizontalmente la gráfica de $f$, $c$ unidades, (multiplicando por $c$ los valores de $x$).
Ejemplo:
- REFLEXION VERTICAL.
- $g_9 ( x ) = − f ( x )$: Refleja o voltea la gráfica de $f$ en el eje $x$ (multiplicando por $−1$ a los valores de $y$ ).
Ejemplo:
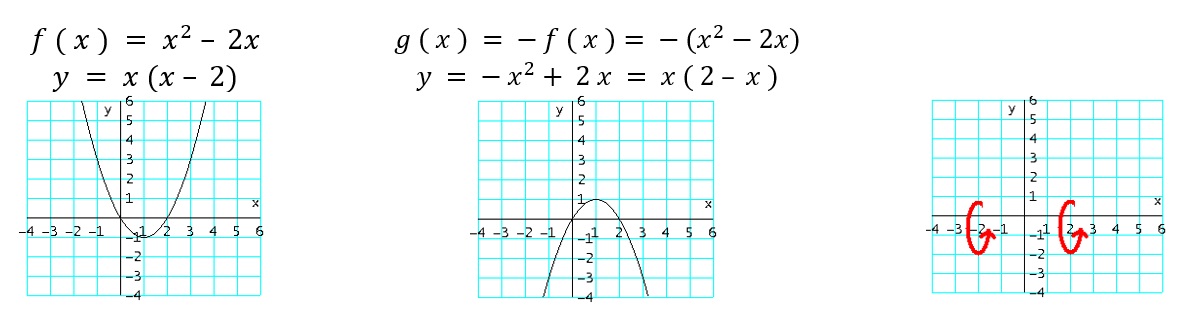
- REFLEXION HORIZONTAL.
- $g_{10} ( x ) = f (− x )$: Refleja o voltea la gráfica de $f$ en el eje $y$ (multiplicando por $−1$ a los valores de $x$ ).
Ejemplo:
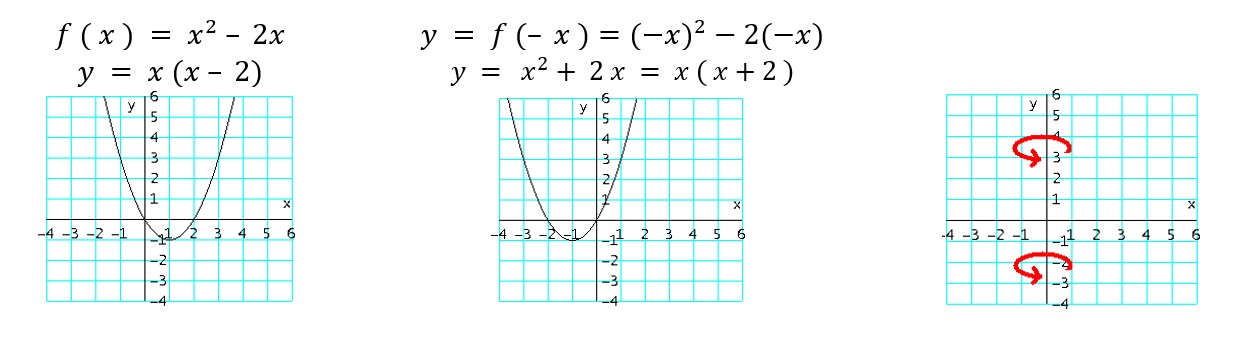
Ejemplo 1
Partiendo de la gráfica $f(x)=sen\;x$ definida solamente en el intervalo $[π, 2π)$, obtener la gráfica de $g(x)=-3sen(-2x+π)+3$ describiendo lasoperaciones gráficas realizadas. También obtener para g(x): el dominio, el rango, los ceros o raíces, la monotonía, la amplitud y suponiendo que estuviera definida en todos los reales cuál sería el periodo.
Iniciamos por factorizar el coeficiente de $x$ en el argumento de la función, para efectuar las operaciones del argumento de izquierda a derecha, son las operaciones que debemos efectuar primero:
$g(x)=-3sen(-2(x-\frac{π}{2}))+3$.
Ahora procedemos a graficar $y=senx$ en el intervalo $[π, 2π)$.
Le aplicamos
Primera operación el signo menos en el argumento: reflejar (voltear) en el eje $y$ la gráfica (multiplicado por -1 los valores de las $x$). Se obtiene $y=g_1(x)=sen(-x)$.
Segunda operación el 2: comprimir horizontalmente en un factor de 2 la gráfica anterior (dividiendo entre 2 los valores de las $x$). Se obtiene $y=g_2(x)=sen(-2x).$
Tercera operación el $-\frac{π}{2}$: translada horizontalmente $\frac{π}{2}$ a la derecha la gráfica anterior (sumando $-\frac{π}{2}$ a los valores de x). Se obtiene $y=g_3(x)=sen(-2(x-\frac{π}{2}))$.
Cuarta operación el 3: alarga verticalmente en un factor de 3 la gráfica anterior (multiplicando por 3 los valores de las $y$). Se obtiene $y=g_4(x)=3sen(-2(x-\frac{π}{2}))$.
Quinta operación el signo menos: refleja (voltea) en el eje $x$ la gráfica anterior (multiplicando por -1 los valores de las $y$). Se obtiene $y=g_5(x)-3sen(-2(x-\frac{π}{2}))$.
Sexta y ultims operación el +3: translada verticalmente 3 unidades hacia arriba, la gráfica anterior (sumando 3 a los valores de las $y$). Se obtiene $y=g_6(x)=-3sen(-2(x-\frac{π}{2}))+3=g(x)$.
De la gráfica de $g(x)$ vemos que:
- El dominio, $D_f=[0,\frac{3}{2π})$.
- El rango, $R_f=[0,6]$.
- Los ceros o raíces, $g(x)=0$ para $x=\frac{π}{4}$.
- La monotonia $f(x)$ es decrececiente para $x∈[-\frac{π}{2},-\frac{π}{4}]$ y para $x∈[\frac{π}{4},\frac{3}{4}π]$
$f(x)$ es creciente para $x∈[-\frac{π}{4},\frac{π}{4}]$ y para $x∈[\frac{3}{4}π,π]$
- La amplitud $a=3$.
- El periodo sería, $P=π.$