Límites laterales
¿Cuánto vale $\underset{x\to 2}{\lim}\sqrt{x-2}$ ? parece no haber problema si $x=2$ entonces $\sqrt{(2)-2}=0$. Pero si se pone atención cuando $x$ tiende a $2$ toma valores como $2.1,\; 1.9,\; 2.01,\; 1.99, . . . $ y $y_1=\sqrt{2.1-2}=\sqrt{.1}≈0.32\;\;\;\; y_2=\sqrt{1.9-2}=\sqrt{-.1} ∉ \mathbb{R}$ entonces $\underset{x\to 2}{\lim}\sqrt{x-2}\; No \;existe$.
Pero si se restringe el acercamiento de $x$ a $2$ únicamente tomando valores mayores que $2$ no habría problema.
En forma análoga a la definición dada para el límite, se pueden definir límites laterales.
Definición intuitiva de límites laterales.
-
El límite lateral derecho $L_1$ de una función $y = f ( x )$ cuando $x$ tiende a $c$ por la derecha,
es el valor al que la función (valor de $y$) se acerca o toma,
cuando x se acerca mucho al valor de $c$ únicamente por la derecha (o sea tomando valores mayores que $c$) sin coincidir nunca con él.
Se denota como:
$\underset{x\to c^+}{\lim}f(x)=L_1$ Ese signo + que aparece como exponente en la c es la notación.
Se lee: el límite de $f ( x )$ cuando $x$ tiende a $c$ por la derecha, es igual a $L_1$.
Nótese que:
- La función debe estar definida en un intervalo a partir de $c$, pudiendo incluirlo o no, ya que $x$ nunca tomará ese valor de $c$.
- El valor de la función debe acercarse tanto como se quiera al valor de $L_1$, tomando el valor de $x$ suficientemente cerca de $c$ por la derecha.
Ejemplo 1
Calcular $\underset{x\to 2^+}{\lim}\sqrt{x-2}$
$\underset{x\to 2^+}{\lim}\sqrt{x-2}=0$
Ejemplo 2
Calcular $\underset{x\to 3^+}{\lim}\frac{|x-3|}{x-3}$
$\underset{x\to 3^+}{\lim}\frac{|x-3|}{x-3}:\frac{0}{0}: indeterminado$
Si $x\rightarrow 3 ^+$ $x$ está tomando valores como $x_1=3.1, \;x_2=3.01,\;...;$ $x>3$
y $x-3>0$ entonces $|x-3|=x-3$
$\underset{x\to 3^+}{\lim}\frac{|x-3|}{x-3}=\underset{x\to 3^+}{\lim}\frac{x-3}{x-3}=\underset{x\to 3}{\lim}1=1$.
Ejemplo 3
Calcular $\underset{x\to 5^+}{\lim}\sqrt{5-x}$
$\underset{x\to 5^+}{\lim}\sqrt{5-x}\;No \;existe$, porque $x$ está tomando valores como $x_1=5.1,\;x_2=5.01,\;...$ y los valores de los $y$ correspondientes no están en los reales.
Ejemplo 4
Calcular $\underset{x\to 1^+}{\lim}\frac{3x^2-4x+1}{-2x^2+2}$
$\underset{x\to 1^+}{\lim}\frac{3x^2-4x+1}{-2x^2+2}:\frac{3-4+1}{-2+2}: indeterminado$
$ L=\underset{x\to 1^+}{\lim}\frac{(x-1)(3x-1)}{(x-1)(-2x-2)}=\underset{x\to 1^+}{\lim}\frac{3x-1}{-2x-2}=\frac{2}{-4}=-\frac{1}{2}$.
- El límite lateral izquierdo $L_2$ de una función $y = f ( x )$ cuando $x$ tiende a $c$ por la izquierda,
es el valor al que la función (valor de $y$) se acerca o toma,
cuando $x$ se acerca mucho al valor de $c$ únicamente por la izquierda (o sea valores menores que $c$) sin coincidir nunca con él.
Se denota como:
$\underset{x\to c^-}{\lim}f(x)=L_2$ Ese signo - que aparece como exponente en la c es la notación.
Se lee: el límite de $f ( x )$ cuando $x$ tiende a $c$ por la izquierda, es igual a $L_2$.
Nótese que:
- La función debe estar definida en un intervalo que contenga a $c$ como extremo derecho, pudiendo incluirlo o no, ya que $x$ nunca tomará ese valor de $c$.
- El valor de la función debe acercarse tanto como se quiera al valor de $L_2$, tomando el valor de $x$ suficientemente cerca de $c$ por la izquierda.
Ejemplo 1
Calcular $\underset{x\to 2^-}{\lim}\sqrt{x-2}$
$\underset{x\to 2^-}{\lim}\sqrt{x-2}=No \; existe$, porque cuando $x\rightarrow 2^-$ está tomando valores como
$x_1=1.9,\; x_2=1.99, \;...$ y los valores de las $y$ correspondientes no están en los reales.
Ejemplo 2
Calcular $\underset{x\to 3^-}{\lim}\frac{|x-3|}{x-3}$
$\underset{x\to 3^-}{\lim}\frac{|x-3|}{x-3}:\frac{0}{0}: indeterminado$
Si $x\rightarrow 3^-$, está tomando valores coo $2.9, \;2.99,\;...x<3$ y $x-3<0$ entonces $|x-3|=-(x-3)$ para qyue el resultado sea positivo.
$L=\underset{x\to 3^-}{\lim}\frac{-(x-3)}{x-3}=\underset{x\to 3^-}{\lim}-1=-1$.
Ejemplo 3
Calcular $\underset{x\to 5^-}{\lim}\sqrt{5-x}$
$\underset{x\to 5^-}{\lim}\sqrt{5-x}=0$, porque $x$ está tomando valores como: $4.9, \;4.99,\;...$
Ejemplo 4
Calcular $\underset{x\to 1^-}{\lim}\frac{3x^2-4x+1}{-2x^2+2}$
$\underset{x\to 1^-}{\lim}\frac{3x^2-4x+1}{-2x^2+2}:\frac{0}{0}: indeterminado$
$L=\underset{x\to 1^-}{\lim}\frac{(x-1)(3x-1)}{(x-1)(-2x-2)}=\frac{3x-1}{-2x-2}=\frac{2}{-4}=\underset{x\to 1^-}{\lim}-\frac{1}{2}$.
- Es claro que si una función tiene límite cuando $x$ tiende $c$, esto es $\underset{x\to c}{\lim} f(x)=L$ entonces los dos límites laterales existen y son iguales a él,
esto es $\underset{x\to c^-}{\lim} f(x)=L$ y $\underset{x\to c^+}{\lim} f(x)=L$.
Y viceversa, si en una función los dos límites laterales son iguales, cuando $x$ tiende a $c$, esto es $\underset{x\to c^+}{\lim}f(x)=L\;\;\;\;$ y $\;\;\;\underset{x\to c^-}{\lim}f(x)=L$
entonces el límite (por los dos lados) existe y es igual a ellos: $\underset{x\to c}{\lim} f(x)=L$.
En cambio, si en una función los límites laterales cuando $x$ tiende a $c$ son diferentes, esto es $\underset{x\to c^+}{\lim}f(x)=L_1\;\;\;$ y $\;\;\;\underset{x\to c^-}{\lim}f(x)=L_2$
con $L_1≠L_2$ entonces el límite (por los dos lados) $\underset{x\to c}{\lim}f(x)\; No\; existe$.
Ejemplo 1
Calcular $\underset{x\to 2}{\lim}\sqrt{x-2}$
$\underset{x\to 2}{\lim}\sqrt{x-2}\; No \; existe$, porque $\underset{x\to 2^-}{\lim}\sqrt{x-2}\;No\;existe$
aunque $\underset{x\to 2^+}{\lim}\sqrt{x-2}=0$.
Ejemplo 2
Calcular $\underset{x\to 3}{\lim}\frac{|x-3|}{x-3}$
$\underset{x\to 3}{\lim}\frac{|x-3|}{x-3}\; No\; existe$ porque $\underset{x\to 3^+}{\lim}\frac{|x-3|}{x-3}=1$ ≠$\underset{x\to 3^-}{\lim}\frac{|x-3|}{x-3}=-1$
Ejemplo 3
Calcular $\underset{x\to 5}{\lim}\sqrt{5-x}$
$\underset{x\to 5}{\lim}\sqrt{5-x}\; No\;existe$, porque $\underset{x\to 5^+}{\lim}\sqrt{5-x}\; No \;existe$ aunque $\underset{x\to 5^-}{\lim}\sqrt{5-x}=0$.
Ejemplo 4
Calcular $\underset{x\to 1}{\lim}\frac{3x^2-4x+1}{-2x^2+2}$
$\underset{x\to 1}{\lim}\frac{3x^2-4x+1}{-2x^2+2}:\frac{3-4+1}{-2+2}=\frac{0}{0}: indeterminado$
$\underset{x\to 1}{\lim}\frac{3x^2-4x+1}{-2x^2+2}=\underset{x\to 1}{\lim}\frac{(x-1)(3x-1)}{(x-1)(-2x-2)}=\underset{h \to 1}{\lim}\frac{3x-1}{-2x-2}=-\frac{1}{2}$ Igual que los dos limites laterales.
Ejemplo 5
Calcular
$L_1=\underset{x\to -2}{\lim}f(x),\;\;\;\;\;\;\;$ $L_2=\underset{x\to 3}{\lim}f(x)$ y $\;\;\;\;\;\;\;L_3=\underset{x\to 0}{\lim}f(x)$ para:
$f(x)=\left\{\begin{matrix}
x^2-6 & si & x ≤-2 \\
2x-1 & si & -2< x < 3 \\
5 & si & 3< x < 4
\end{matrix}\right.$
La representacion gráfica de los tres intervalos donde está definida la funcion es:
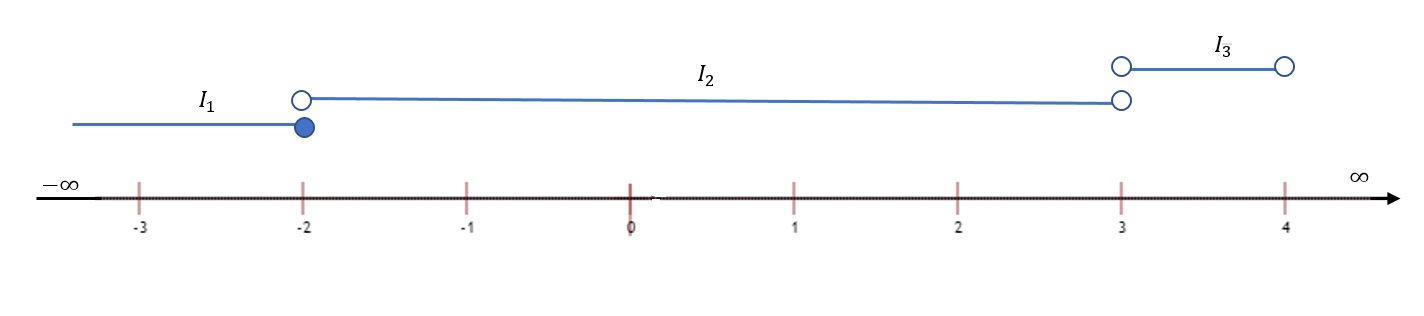
el dominio de la función es $D_f=(-\infty, 3) \cup (3,4)$.
Para calcular $L_1$ , se debe saber qué expresión se va a tomar para $f(x)$ y se observa que en el intervalo $(-\infty, -2] $, $f (x)=x^2-6$ y en el intervalo $(-2,3)$, $f (x)=2x-1$ entonces la izquierda debe $-2$ está en el primer intervalo y la derecha de $-2$ está en el segunda intervalo.
Entonces se deben calcular limites laterales.
$ L_{1,1}=\underset{x\to -2^-}{\lim}f(x)=\underset{x\to -2^-}{\lim}x^2-6=4-6=-2\;\;\;$ y
$ L_{1,2}=\underset{x\to -2^+}{\lim}f(x)=\underset{x\to -2^+}{\lim}2x-1=-4-1=-5\;\;\;$
como $L_{1,1}≠ L_{1,2}$ (limites laterales diferentes) el $\underset{x\to -2}{\lim}No\;existe.$
Para calcular $L_2$ se tiene que el intervalo $(-2,3)$, $f(x)=2x-1$ y en el intervalo $(3,4),$ $f(x)=5$, se calculan límites laterales
$ L_{2,1}=\underset{x\to 3^-}{\lim}f(x)=\underset{x\to 3^-}{\lim}2x-1=5\;\;\;$ y
$ L_{2,2}=\underset{x\to 3^+}{\lim}f(x)=\underset{x\to 3^+}{\lim}5=5\;\;\;$
como $L_{2,1}=L_{2,2}$ (limites laterales iguales) el $\underset{x\to 3}{\lim}5=5$.
Para calcular $L_3$ se tiene $x=0\; ∈\;(-2,3), \; f(x)=2x-1$ entonces $\underset{x\to 0}{\lim}f(x)=\underset{x\to 0}{\lim}2x-1=-1.$
Si se traza la gráfica de la función se puede visualizar los tres límites
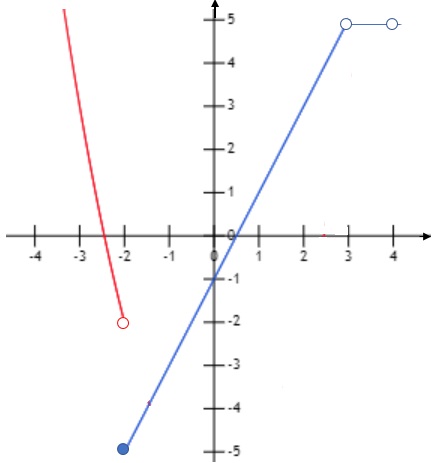
$\underset{x\to -2}{\lim}f(x)\;No \; existe$ por que $\underset{x\to -2^-}{\lim}=-2\;\;$ y $\underset{x\to -2^+}{\lim}=-5\;\;$
$\underset{x\to 3}{\lim}f(x)=5$ notese que $f(3)\;No\; existe\; x=3∉ D_f.$
$\underset{x\to 0}{\lim}f(x)=-1.$




