Límites de valor infinito y en infinito
Límites infinitos
El concepto de límite se puede ampliar y tener como resultado infinito o menos infinito.
Se dijo que:
El límite $L$ de una función $y = f ( x )$ cuando $x$ tiende a $c$,
es el valor al que la función (valor de $y$) se acerca o toma,
cuando $x$ se acerca al valor de $c$, sin coincidir nunca con él.
Se denota como:
$$\lim_{x \rightarrow c}f(x)=L$$
Se lee: el límite de $f ( x )$ cuando $x$ tiende a $c$ es igual a $L$.
Ahora se permitirá que $L$ sea infinito o menos infinito.
Por ejemplo si consideramos la función $f(x)=\frac{1}{x}$ ¿qué pasa con el valor de y conforme $x$ tiende a cero?
Viendo la gráfica de la función:
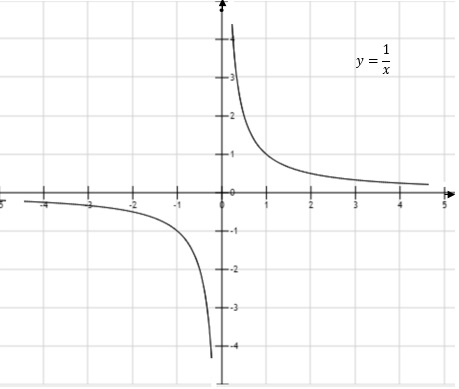
se observa que:
- del lado derecho de $x=0$ los valores de y están muy arriba, entonces se establece que el límite lateral derecho
$\underset{x\to0^+}{\lim}\frac{1}{x}=\infty$, nótese que su cálculo sería $\underset{x\to 0^+} {\lim}\frac{1}{x}=\frac{1}{0^+}=\infty$.
y
- del lado izquierdo de $x=0$ los valores de y están muy abajo, entonces se establece que el límite lateral izquierdo
$\underset{x\to0^-}{\lim}\frac{1}{x}=-\infty$, nótese que su cálculo sería $\underset{x\to0^-}{\lim}\frac{1}{x}=\frac{1}{0^-}=-\infty$ .
Entonces el $\underset{x\to0}{\lim}$ $\frac{1}{x}$ no existe porque los límites laterales son diferentes.
En general, cuando al calcular un límite se llega a una expresión del tipo $\frac{cte≠0}{0}$ se dice que es indefinida, y hay que determinar el signo del denominador, frecuentemente calculando límites laterales; el resultado del límite nada más puede ser infinito positivo o negativo,
según sean los signos del numerador y del denominador.
(Se tiene que: $\frac{+}{+}=+$, $\;\;\frac{-}{-}=+$, $\;\;\frac{+}{-}=-\;\;$ y $\;\;\frac{-}{+}=-$ ).
El límite no existe en caso de que el denominador se vaya a cero tomando valores positivos y negativos, como en el caso anterior.
Nótese que:
- Esto coincide con la experiencia aritmética de dividir una constante diferente de cero entre un valor muy muy cerca de cero, el resultado será muy grande, tan grande como se quiera,
escogiendo el denominador suficientemente cerca de cero. Por ejemplo $\frac{-7}{-0.0001}=70000$.
- Al tender a cero una cantidad puede hacerlo tomando valores positivos y negativos por eso frecuentemente es necesario calcular límites laterales para determinar el signo del denominador.
- Esta indefinición $\frac{cte≠0}{0}$ al calcular un límite es fundamentalmente diferente de la indeterminación $\frac{0}{0}$ en la que hay que trabajar algebraicamente la función para removerla.
Ejemplo 1
Calcular:
$$\lim_{x \rightarrow 3}\frac{4-x^2}{x^2-6x-9}$$
$$L=\lim_{x \rightarrow 3}\frac{4-x^2}{x^2-6x-9}:\frac{4-9}{9-18+9}=\frac{-5}{0}:\left\{\begin{matrix}
\infty\\
-\infty
\end{matrix}\right.$$
$$L=\lim_{x \rightarrow 3}\frac{4-x^2}{{(x-3)}^2}=\frac{-5}{0^+}=-\infty$$
Ejemplo 2
Calcular:
$$\lim_{x \rightarrow 2}\frac{3x-2}{x^2-4}$$
$$L=\lim_{x \rightarrow 2}\frac{3x-2}{x^2-4}:\frac{4}{0}:\left\{\begin{matrix}
\infty\\
-\infty
\end{matrix}\right.$$
Hay que calcular límites laterales para deteminar el signo en el denominador.
$$\lim_{x \rightarrow 2^+}\frac{3x-2}{x^2-4}=\frac{4}{0^+}=\infty\;\;\;\;\;\;(\frac{+}{+}=+)$$
y
$$\lim_{x \rightarrow 2^-}\frac{3x-2}{x^2-4}=\frac{4}{0^-}=-\infty\;\;\;\;\;\;(\frac{+}{-}=-)$$
Entonces el $\lim_{x \rightarrow 2}\frac{3x-2}{x^2-4}\;\;\;No\;existe$ por que los límites laterales son diferentes.
Límites en infinito.
Otra extensión del concepto de límite $\underset{x\to c}{\lim} f(x)=L$ es cuando el valor de $\;c\;$ es infinito ($x$ tiende a infinito) positivo o negativo.

En la gráfica anterior de la función $y=f(x)=\frac{1}{x}$
¿Qué pasa con el valor de $y$ cuando $ x$ está muy a la derecha?
Se observa que el valor de $y$ está cerca de cero, más cerca de cero conforme el valor de $x$ esté más a la derecha, se establece que $\underset{x\to \infty }{\lim}\frac{1}{x}=0$ .
Nótese que el cálculo sería $\underset{x\to \infty }{\lim}$ $\frac{1}{x}=\frac{1}{\infty}=0$.
¿Qué pasa con el valor de $y$ cuando $x$ está muy a la izquierda?
Se observa que el valor de $y$ está cerca de cero, más cerca de cero conforme el valor de $x$ esté más a la izquierda, esto se establece como $\underset{x\to -\infty }{\lim}\frac{1}{x}=0$ .
Nótese que el cálculo sería $\underset{x\to -\infty }{\lim}$ $\frac{1}{x}=\frac{1}{-\infty}=0$.
En general, cuando al calcular un límite se llegue a la expresión $\frac{cte}{\infty}$ el resultado es cero
cualquiera que sea el valor de la constante. Esto coincide con la experiencia aritmética de dividir una constante, entre un valor mucho más grande,
el resultado estará cerca de cero, por ejemplo $\frac{-2.7}{10000}=-0.00027 $.
Ejemplo 1
Calcular:
$$\lim_{x \rightarrow \infty}\frac{3x^2+x-4}{x^2-1}$$
Ahora se tiene que operar con infinito, recuérdese que infinito no es un número sino un concepto que da información numérica;
así se puede pensar que es un número muy grande, pero móvil.
Entonces infinito al cuadrado es infinito, porque un número muy grande elevado al cuadrado da otro número muy grande.
Y así: infinito multiplicado por 3 es infinito, en general infinito multiplicado por cualquier constante positiva será infinito y
multiplicado por una constante negativa será menos infinito; se conservan las reglas de los signos.
Infinito más infinito es infinito.
Infinito menos 4 es infinito, infinito menos cualquier constante es infinito, pero infinito menos infinito es indeterminado porque ya no es claro dar un resultado.
En este límite se tiene infinito entre infinito, no es claro dar un resultado, porque qué tan grande es un infinito con respecto al otro, así también es indeterminado, entonces se debe
manipular algebraicamente la función para remover la indeterminación.
$$\lim_{x \rightarrow \infty}\frac{3x^2+x-4}{x^2-1}:\frac{\infty}{\infty}: indeterminado$$
$$\lim_{x \rightarrow \infty}\frac{3x^2+x-4}{x^2-1}=\lim_{x \rightarrow \infty}\frac{x^2(3+\frac{1}{x}-\frac{4}{x^2})}{x^2(1+\frac{1}{x^2})}=\lim_{x \rightarrow \infty}\frac{3+\frac{1}{x}-\frac{4}{x^2}}{1+\frac{1}{x^2}}=\frac{3+0-0}{1+0}=3$$
Nótese que la técnica para calcular este tipo de límite, consiste en factorizar forzadamente la $x$ de mayor potencia tanto en el numerador como en el denominador y hacer la simplificación correspondiente para quitar la indeterminación.
Puede verse también como dividir entre la $x$ de mayor potencia tanto el numerador como el denominador, es análogo.
Ejemplo 2
Calcular:
$$\lim_{x \rightarrow \infty}\frac{2x+\sqrt{x^2+5x-2}}{4-2x}$$
$$L=\lim_{x \rightarrow \infty}\frac{2x+\sqrt{x^2+5x-2}}{4-2x}:\frac{\infty}{-\infty}:\;indeterminado$$
$$L=\lim_{x \rightarrow \infty}\frac{x(2+\sqrt{1+\frac{5}{x}-\frac{2}{x^2}})}{x(\frac{4}{x}-2)}=\lim_{x \rightarrow \infty}\frac{2+\sqrt{1+\frac{5}{x}-\frac{2}{x^2}}}{\frac{4}{x}-2}=\frac{2+\sqrt{1+0-0}}{0-2}=\frac{3}{-2}=-\frac{3}{2}.$$
Notese que:
$$\sqrt{x^2+5x-2}=\sqrt{x^2(1+\frac{5}{x}-\frac{2}{x^2})}=\sqrt{x^2}\sqrt{1+\frac{5}{x}-\frac{2}{x^2}}=$$
$$=|x|\sqrt{1+\frac{5}{x}-\frac{2}{x^2}}=x\sqrt{1+\frac{5}{x}-\frac{2}{x^2}}$$
Ya que si $x \rightarrow \infty,\;\;\;\;x>0\;\;\; y\;\;\; |x|=x$.
Ejemplo 3
Calcular:
$$\lim_{x \rightarrow -\infty}x^2+x-2:\infty-\infty:\;indeterminado$$
$$L=\lim_{x \rightarrow -\infty}x^2(1+\frac{1}{x}-\frac{2}{x^2})=\infty(1+0-0)=\infty.$$
Nótese que $f(x)=x^2+x-2$ graficamente es una parábola que abre hacia arriba y entonces cuando $x \rightarrow -\infty$ los valores correspondientes de $y \rightarrow \infty$.
Ejemplo 4
Calcular:
$$\lim_{x \rightarrow \infty} (2x-\sqrt{4x^2-2x+10\;}\;):\; \infty-\sqrt{\infty-\infty}\;\;:indeterminado$$
$$L=\lim_{x \rightarrow \infty}x(2-\sqrt{4-\frac{2}{x}+\frac{10}{x^2}}\;\;):\infty(-0)\;\;:indeterminado$$
porque es un número muy grande multiplicado por otro que se acerca a cero entonces depende de la forma en que uno se va a infinito y el otro se va a cero.
En este tipo de casos hay que racionalizar como sigue :
$$L=\lim_{x \rightarrow \infty}(2x-\sqrt{4x^2-2x+10\;}).(\frac{2x+\sqrt{4x^2-2x+10\;}}{2x+\sqrt{4x^2-2x+10\;}})=$$
$$=\lim_{x \rightarrow \infty}\frac{4x^2-(4x^2-2x+10)}{2x+\sqrt{4x^2-2x+10\;}}=\lim_{x \rightarrow \infty}\frac{2x-10}{2x+\sqrt{x^2(4-\frac{2}{x}+\frac{10}{x^2})\;}}=$$
$$=\lim_{x \rightarrow \infty}\frac{x(2-\frac{10}{x})}{x(2+\sqrt{4-\frac{2}{x}+\frac{10}{x^2}}\;)}=\frac{2-0}{2+\sqrt{4-0+0\;}\;}=\frac{2}{4}=\frac{1}{2}.$$
Se puede comprobar numéricamente valorando por ejemplo $$f(1000)=2(1000)-\sqrt{4(1000)^2-2(1000)+10}≈ 0.4975619$$
Que es aproximadamente el valor obtenido del límite, lo que nos permite pensar que es correcto.




