


Un ángulo es la abertura entre dos segmentos de rectas o rayos, llamados lados del ángulo, que parten de un punto común llamado vértice como se muestra en la figura:
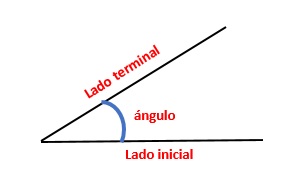
A uno de los lados se le llama lado inicial y al otro lado terminal.
Los ángulos pueden medirse en grados, de acuerdo con la convención de que un grado es la trescientosesentava parte del ángulo de una vuelta completa, cuando el lado terminal coincide con el inicial.
Los ángulos también pueden medirse en radianes, donde la medida de una vuelta completa equivale a $2π ≈ 6.2816$ radianes, esto es, el número de veces que cabe el radio en la circunferencia, cualquiera que ésta sea.
En general la medida de un ángulo en radianes se define como el cociente de la longitud del arco de la circunferencia definida por el ángulo, con centro en su vértice, dividida sobre la longitud del radio de esa circunferencia.
En las siguientes figuras se muestran algunos ángulos con su medida en grados y en radianes.
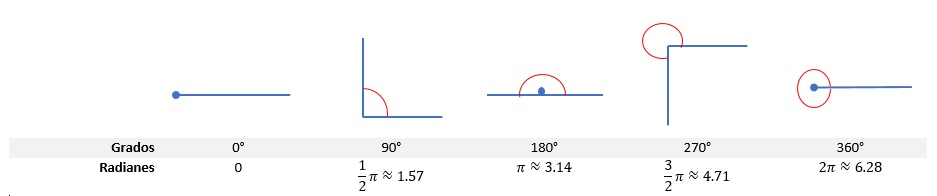
Nótese que la medida en grados se denota con el símbolo ° y siempre debe indicarse, sin embargo los radianes al provenir del cociente de dos longitudes carece de unidades.
En un triángulo rectángulo donde se fija un ángulo $θ$ como se ve en la figura
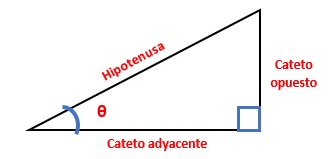
Las funciones seno, coseno, tangente, cotangente, secante y cosecante se denotan y se definen como sigue:

Nótese que el ángulo $θ$ puede variar entre cero y 90 grados: $0$° ‹ $θ$ ‹ $90$°; o entre cero y $π/2$ radianes: $0$ ‹ $θ$ ‹ $π/2$, según el triángulo que se trace. Y que una vez que se conoce el seno y el coseno, todas las demás funciones quedan definidas en términos de ellas.
Si ahora se considera un círculo de radio uno con centro en el origen $O$ de un sistema de ejes coordenados $“ t-y ”$ en el primer cuadrante, un punto $P$ en el círculo, determina un ángulo $x$, tomando como lado inicial al radio del círculo en el eje horizontal y lado terminal al segmento $OP$.
Bajando una perpendicular desde el punto $P$ al eje horizontal $t$ se define el punto $A$ y se tendrá un triángulo rectángulo $OPA$, en él pueden establecerse las funciones $sen$ $x$ y $cos$ $x$, tal como se definieron anteriormente, para el ángulo $x$ determinado por el punto $P$, que puede variar entre cero y $π/2$ radianes, ver figura
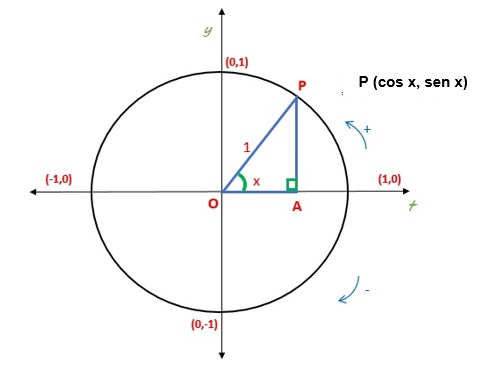
Se tiene que la hipotenusa es uno, entonces la función seno de $x$, que se denota como $sen$ $x$, es igual a la ordenada del punto $P$ y la función coseno de $x$, que se denota como $cos$ $x$ es igual a la abscisa de ese punto $P$.
Se define ahora la función seno como la ordenada del punto $P$ y la función coseno como la abscisa de ese punto $P$ independientemente del triángulo.
Y al mover el punto $P$ en el círculo se pueden extender los valores del ángulo $x$.
El ángulo se define como positivo cuando se mide del sentido positivo del eje horizontal al sentido positivo del eje vertical, y será negativo cuando se mida en sentido contrario, o sea del sentido positivo del eje horizontal al sentido negativo del eje vertical.
Como el punto $P$ puede dar muchas vueltas en el círculo en los dos sentidos, positivo y negativo, los valores de $x$ irán desde menos infinito hasta infinito: $-\infty$ < $x$ < $\infty$ y las funciones seno y coseno tendrán como dominio todos los reales $\mathbb{R}$ .
Ubicando al punto $P$ para $x = 0$ , $± π/2$, $±π$ , $±(3/2)π$, $±2π$, $±(5/2)π$, $±3π$, etc. y viendo sus coordenadas, se tienen de manera inmediata los valores del seno y el coseno para esos ángulos.
Los valores que toman las funciones $sen$ $x$ y $cos$ $x$ varían entre menos uno y uno: $-1≤$ $sen$ $x$ $≤1$ y $-1≤$ $cos$ $x$ $≤1$.
Se tiene que en cada vuelta del punto $P$ en el círculo, se repiten los valores tomados, por lo que las funciones son peródicas, tienen periodo $2π$, esto es $sen ( x ) = sen ( x + 2π ) $ y $cos ( x ) = cos ( x + 2π )$.
Intuitivamente se puede ver que para un pequeño moviendo del punto $P$ en el círculo, se tiene un pequeño aumento o disminución en sus coordenadas (abscisa y ordenada) que son los valores de las funciones coseno y seno, por lo que podemos ver que son funciones continuas (a reserva de demostrarlo posteriormente).
Ahora se puede pasar a esbozar las gráficas y determinar algunos de sus elementos. Empecemos por $y = sen$ $x$ (ordenada del punto $P$ en el círculo unitario):
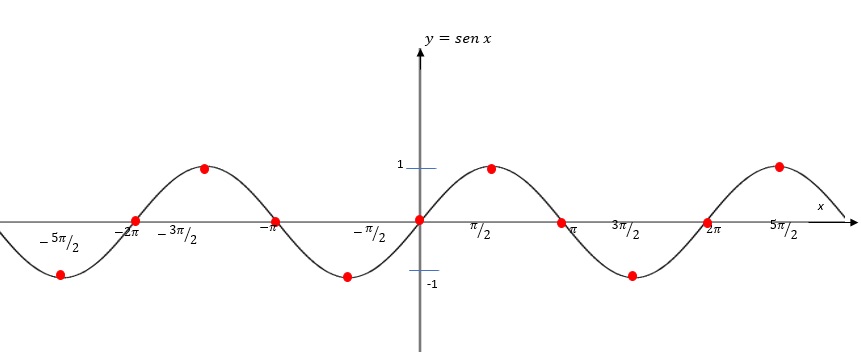
Se ve que la gráfica es simétrica con respecto al origen, la función es impar, esto es $sen$ $( – x ) = – sen$ $( x )$.
Como se ve y ya se había mencionado la función tiene periodo $P=2π$, los valores de la función se repiten en cada intervalo de longitud $2π$ en el eje $x$.
Para la función y = cos x (abscisa del punto $P$ en el círculo unitario):
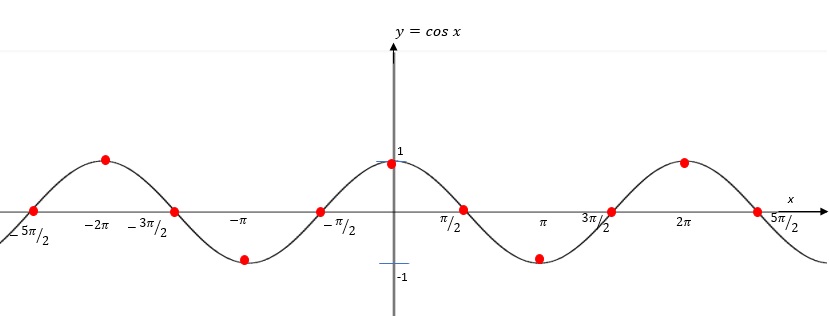
Se ve que la gráfica es simétrica con respecto al eje $y$ la función es par, esto es: $cos\; (\; – x \;) = cos\; ( \;x\; )$.
Como se ve y ya se había mencionado la función tiene periodo $P$=2π , los valores de la función se repiten en cada intervalo de longitud $2π$ en el eje $x$.
Fijándose en el triángulo $OAP$ de la definición de las funciones en el círculo unitario y aplicando el teorema de Pitágoras se tiene que $sen^2x+cos^2x=1$.
En forma análoga, se pueden considerar triángulos rectángulos en los otros cuadrantes, y aunque el seno es la ordenada y el coseno es la abscisa del punto $P$ y no la longitud de los lados, al tomar el cuadrado es equivalente; por lo que la identidad $sen^2x+cos^2x=1$ es válida para todo valor de $x$.
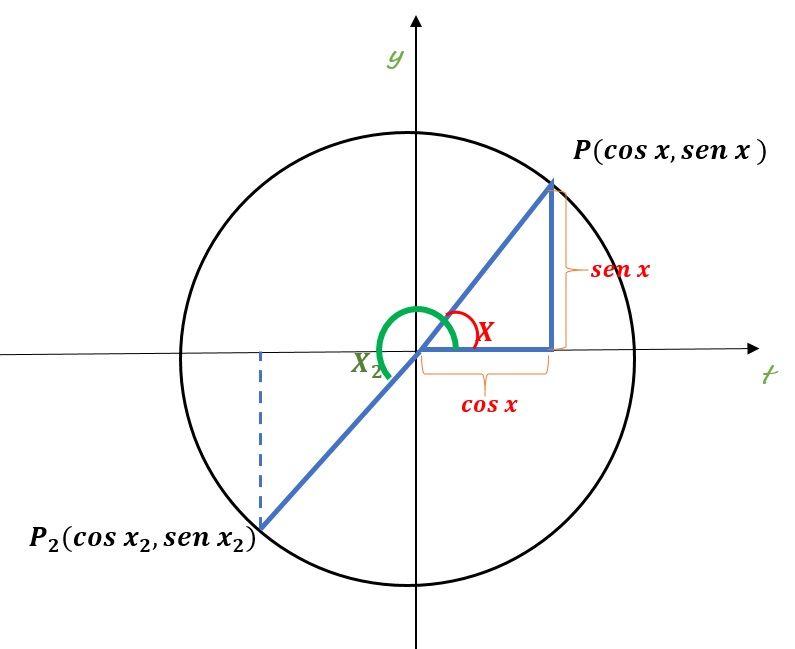
Se puede demostrar (ya no de manera tan inmediata ) que:
$sen (a+b) = sen (a) cos (b) + cos (a) sen (b)$.A partir de estas tres identidades básicas se pueden obtener muchas otras.
Por ejemplo: $sec^2(x)+tan^2(x)=1$ Porque $sec^2(x)= \frac{1}{cos^2(x)}$ y si se multiplica por uno expresado como $sen^2(x)+cos^2(x)$ no se altera la cantidad y entonces: $sec^2(x)=\frac{1}{cos^2(x)}(sen^2(x)+cos^2(x))=\frac{cos^2(x)+sen^2(x)}{cos^2(x)}=1+tan^2(x)$.
Y así muchas otras.