Ejemplos Numérico Algebraico
$\boldsymbol{8 > 0}$ $\boldsymbol{-2x > 4}$
$\boldsymbol{8\color{red}{(-\frac{1}{2})} < 0\color{red}{(-\frac{1}{2})}}$ $\boldsymbol{-2x\color{red}{(-\frac{1}{2})} < 4\color{red}{(-\frac{1}{2})}}$
$\boldsymbol{-4 < 0}$ $\boldsymbol{x < -2}$
CORRECTO Gráficamente:
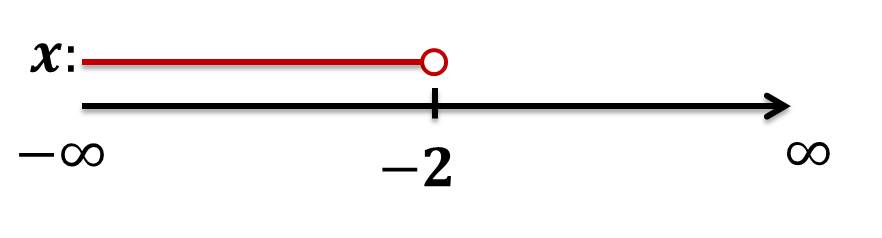
Como intervalo: $\boldsymbol{x\in(-\infty,-2)}$
$\boldsymbol{-4 > -6}$ $\boldsymbol{-3x > -7}$
$\boldsymbol{-4\color{red}{(-\frac{1}{3})} < -6\color{red}{(-\frac{1}{3})}}$ $\boldsymbol{-3x\color{red}{(-\frac{1}{3})} < -7\color{red}{(-\frac{1}{3})}}$
$\boldsymbol{\frac{4}{3} < 2}$ $\boldsymbol{x < \frac{7}{3}}$
CORRECTO Gráficamente:
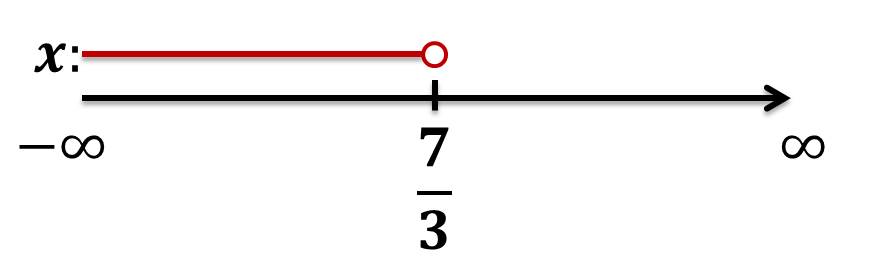
Como intervalo: $\boldsymbol{x\in(-\infty,\frac{7}{3})}$
Desigualdades Lineales
Para resolver una desigualdad lineal se aplican las tres propiedades anteriores para despejar la variable en cuestión.
Ejemplos:
1) $3x-2\leq4 $ En forma abreviada se dice que el 2 que está restando, pasa para el otro lado sumando.
$3x-2\color{red}{+2} \leq 4\color{red}{+2}$
$3x \leq 6$ En forma abreviada se dice que el 3 que está multiplicando, pasa para el otro lado dividiendo.
$3x \color{red}{(\frac{1}{3})} \leq 6\color{red}{(\frac{1}{3})} $
$x \leq 2$
Gráficamente:
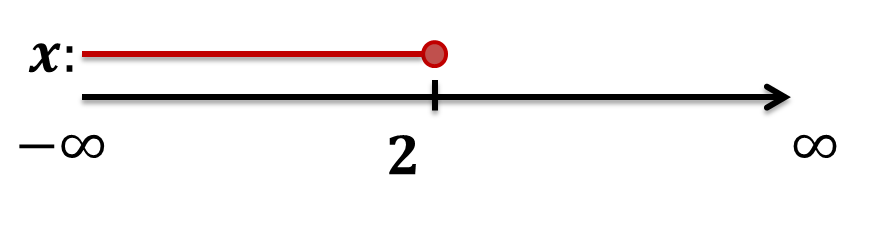
Otro ejemplo:
2) $8-2x < 3$ Como el 8 está sumando, pasa para el otro lado restando.
$-2x <3\color{red}{-8}$
$-2x<-5$ Como el −2 está multiplicando pasa para el otro lado dividiendo y como es negativo invierte el sentido de la desigualdad.
$x > \frac{-5}{\color{red}{-2}}$
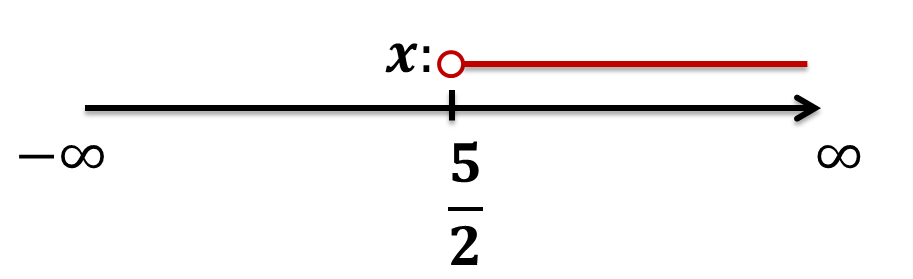
$x > \frac{5}{2}$
Gráficamente: