


Si el límite de la función cuando $x$ tiende a infinito o menos infinito es igual a una constante, entonces la función tiene una asíntota horizontal de ecuación: $y$ igual a la constante, esto es:
Si $\underset{x\to-\infty}{\lim} f(x)=k$ entonces $y=k$ es una asíntota horizontal de $f(x)$.
Si $\underset{x\to\infty}{\lim} \;f(x)=p$ entonces $y=p$ es una asíntota horizontal de $f(x)$.
 |
 |
|---|---|
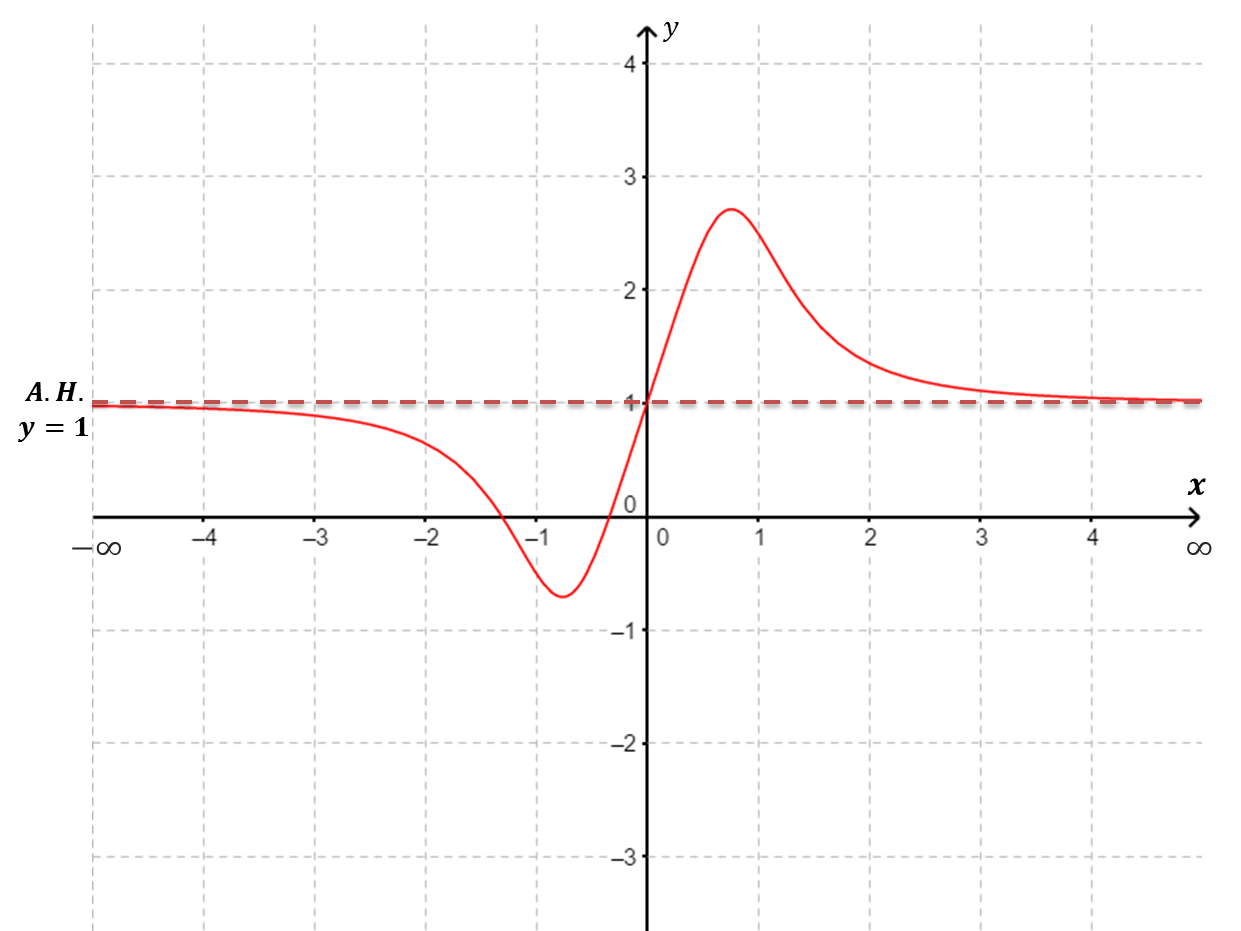
| $f(x)$ tiene una asíntota horizontal de ecuación y=1 $\underset{x\to \infty}{\lim} f(x)=1$ y $\underset{x\to -\infty}{\lim} f(x)=1$. |
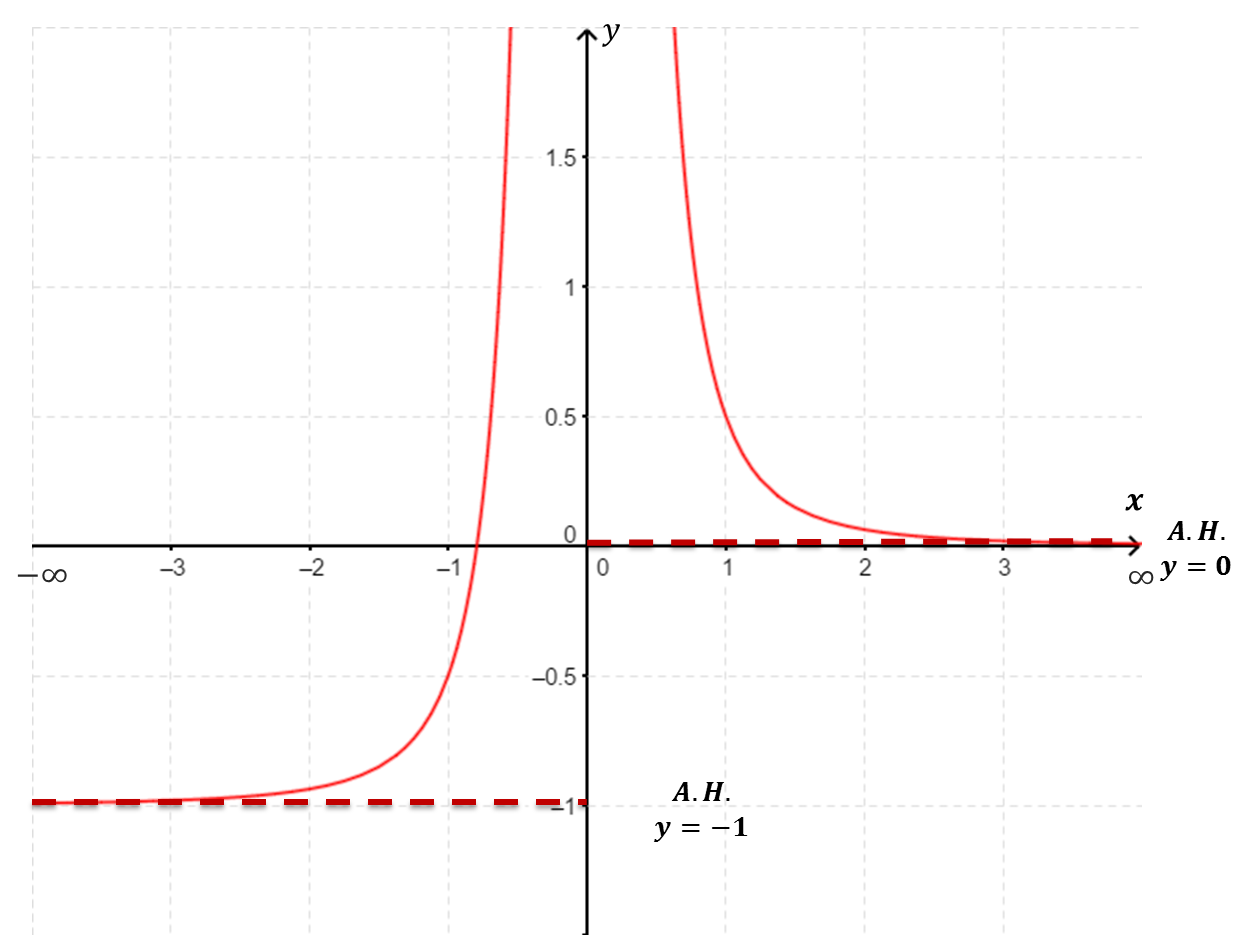
$f(x)$ tiene una asíntota horizontal de ecuación $y=-1$ y $y=0$ $\underset{x\to \infty}{\lim} f(x)=0$ y $\underset{x\to -\infty}{\lim} f(x)=-1$. |
Si el límite de la función cuando $x$ tiende a una constante (valores de $x$ que genere una división entre cero en la función) es igual a infinito positivo o negativo (aunque sea en forma lateral), entonces la función tiene una asíntota vertical de ecuación $x$ igual a la constante, esto es:
Si $\underset{x\to m}{\lim} \;f(x)=\infty$, $\underset{x\to m}{\lim} \;f(x)=-\infty$, o $\underset{x\to m}{\lim} \;f(x)=\not\exists $, con límites laterales infinitos.
Entonces $x=m$ es una asíntota vertical de $f(x)$.
($m$ es un valor de $x$ que genera una división entre cero en la función)
 |
 |
|---|---|
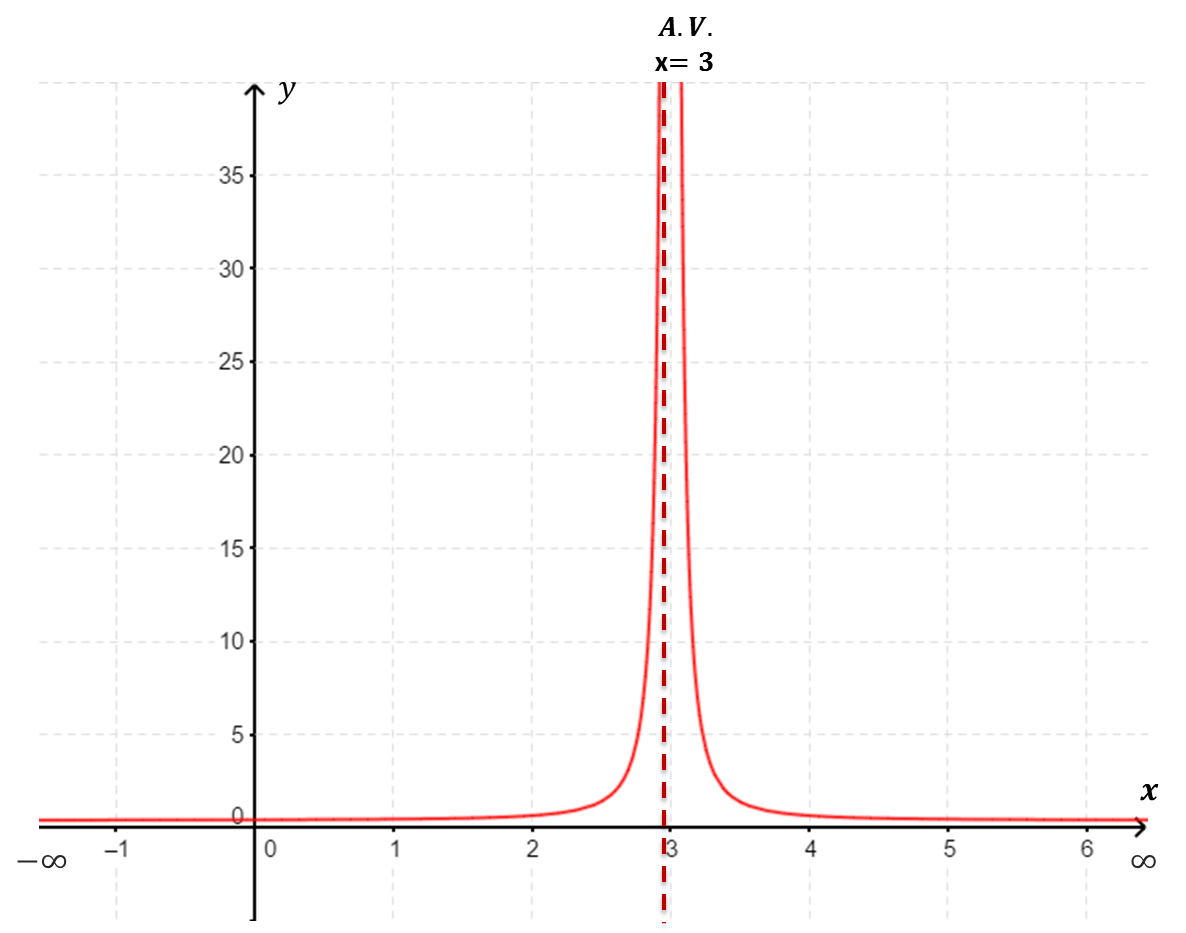
| $f(x)$ tiene una asíntota vertical de ecuación $x=3$ ( $\underset{x\to 3}{\lim} \;f(x)=\infty$). | $f(x)$ tiene una asíntota vertical de ecuación $x=2$ ( $\underset{x\to 2^{+}}{\lim} f(x)=-\infty$ y $\underset{x\to 2^{-}}{\lim} f(x)=\infty$) |